1.2. Уравнения Максвелла для медленно движущихся
сред и их решение
Уравнения Максвелла для неподвижной среды
обычно записываются в дифференциальной форме и имеет вид:
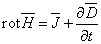 (1.4)
(1.4)
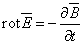
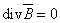
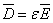 ; ;
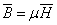 ; ;
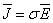 .
(1.5) .
(1.5)
В медленно движущихся средах (скорость
v много меньше скорости света с)
составляющие электромагнитного поля меняются в зависимости от точки наблюдения
или системы принятых координат.
Если принять систему координат неподвижной
в пространстве, то с точки зрения неподвижного наблюдателя в движущейся среде
выражение для плотности тока приобретает новый вид:
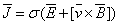 (1.6)
(1.6)
Если принять систему координат, движущуюся
совместно с движущимся телом (жестко связанную с этим телом), то выражение для
плотности тока будет как в (1.5). Решение при этом получается проще. Однако при
переходе к неподвижной системе координат, что всегда желательно иметь,
приходится переходить к новой частоте, определяемой относительной скоростью.
Токами смещения из-за их малости по
сравнению с токами производимости всегда можно пренебречь и основные уравнения
упрощаются:
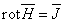 ; ;
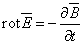 ; ;
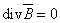 (1.7)
(1.7)
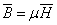
В неподвижной системе координат, которой мы
будем пользоваться, окончательно уравнения Максвелла имеют вид:
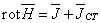 (1.8)
(1.8)
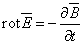 (1.9)
(1.9)
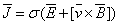 (1.10)
(1.10)
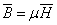 (1.11)
(1.11)
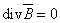 (1.12)
(1.12)
Здесь и выше, конечно,
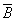 , ,
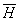 , ,
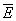 , ,
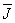 —
векторы магнитной индукции, напряженности магнитного поля, напряженности
электрического поля и плотности тока, —
векторы магнитной индукции, напряженности магнитного поля, напряженности
электрического поля и плотности тока,
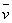 —
вектор скорости движения среды относительно принятой системы координат. —
вектор скорости движения среды относительно принятой системы координат.
В уравнение (1.8) введена плотность тока от
сторонних ЭДС, которая не является индуцированной и поэтому может всегда
считаться заданной.
Вектор результирующей напряженности в
(1.10) содержит две составляющих:
Е — напряженность, обусловленная
изменением поля во времени, или по терминологии, принятой в электрических
машинах, трансформаторной ЭДС. 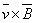 —
напряженность, обусловленная движением в магнитном поле, или по той же аналогии,
ЭДС движения. —
напряженность, обусловленная движением в магнитном поле, или по той же аналогии,
ЭДС движения.
Легко проверить, что при переходе к
движущейся системе координат, в которой
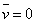 система
уравнений (1.8–1.12) переходит в (1.7), так как плотность тока
J не изменяется в различных системах координат
(эта величина является физической реальностью). Величины электрической
проводимости σ, магнитной проницаемости μ и скорости
v всегда считаются заданными и при решении
уравнений Максвелла неизвестными оказываются В, Н, Е, J. Так как
количество неизвестных равно числу основных уравнений все неизвестные
определяются полностью. Постоянные интегрирования определяются дополнительно из
граничных условий. система
уравнений (1.8–1.12) переходит в (1.7), так как плотность тока
J не изменяется в различных системах координат
(эта величина является физической реальностью). Величины электрической
проводимости σ, магнитной проницаемости μ и скорости
v всегда считаются заданными и при решении
уравнений Максвелла неизвестными оказываются В, Н, Е, J. Так как
количество неизвестных равно числу основных уравнений все неизвестные
определяются полностью. Постоянные интегрирования определяются дополнительно из
граничных условий.
Нахождение неизвестных осуществляется
последовательным исключением других неизвестных обычным способом и здесь будут
приведены дифференциальные уравнения для отдельных величин поля в окончательном
виде.
Уравнение для
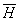
 (1.13)
(1.13)
Уравнение для
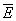
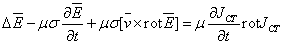 (1.14)
(1.14)
Уравнение для
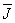
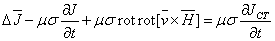 (1.15)
(1.15)
Уравнение (l.15)
значительно сложнее, чем для 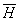 и и
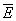 ,
так как в него входит неизвестная величина ,
так как в него входит неизвестная величина
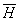 ,
стоящая под знаком сложной функции. По этой причине обычно его не решают, а
плотность тока J определяют по (1.13) и (1.8). ,
стоящая под знаком сложной функции. По этой причине обычно его не решают, а
плотность тока J определяют по (1.13) и (1.8).
|
