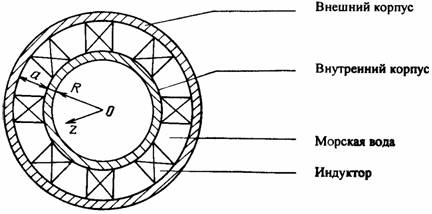
4.1. МГД–движители индукционного типа

В последние годы проявляется научный и технический интерес к проблеме применения на крупнотоннажных морских судах и больших подводных лодках движителей магнитогидродинамического типа. В первую очередь это объясняется ухудшением экономических и массогабаритных показателей гребных винтов при переходе на повышенные скорости.

При создании МГД–движителей используются те же принципы, которые лежат в основе работы кондукционных и индукционных насосов. Разрабатываются также МГД–движители, не имеющие прямых аналогов с электромагнитными насосами. По сравнению с гребными винтами МГД–движители имеют следующие преимущества: непосредственное использование электроэнергии судна для создания тяги, пониженные уровни вибраций и гидродинамических шумов. При больших мощностях атомных энергетических установок и использовании МГД–генераторов для преобразования тепловой энергии реактора в электрическую массогабаритные показатели гребных электрических двигателей оказываются неудовлетворительными. Поэтому альтернативой такому положению может явиться применение магнитогидродинамических движителей.

Примером такого двигателя может служить схема, разработанная применительно к большой подводной лодке и представленная на рис. 4.1. Индукторы, создающие бегущее магнитное поле от носа к корме подводной лодки, расположены между внешним и внутренним корпусами лодки.

Рис. 4.1

В морской воде между корпусами лодки будут индуцироваться токи, замыкающиеся по окружностям, параллельным корпусу лодки. Взаимодействие индуцированных в морской воде токов с магнитным полем приводит к появлению электромагнитных сил, направленных в сторону кормы лодки. Сумма всех пондеромоторных сил создает тяговый упор и лодка приходит в движение.

Длина подводной лодки существенно больше ее поперечных размеров и задача сводится в математическом плане к рассмотрению бесконечно длинного цилиндра с бегущим магнитным полем, нормальная составляющая которого на поверхности цилиндра направлена по радиусу и может быть задана в виде

,                                (4.1)

где В_т – максимальное значение индукции; w₁ – угловая частота; ; t – полюсное деление.

Линейная скорость поля равна  или , где f₁– частота питающего тока.

Из уравнения индукции (1.7)

получаем уравнение

,                              (4.2)

так как если учитывать только осевую компоненту скорости и нормальную составляющую индукции

.                                 (4.3)

По порядку величины отношение левой части уравнения (2.10) к правой равно , где L – длина подводной лодки. При L = 100 м, , ,  величина  имеет порядок 10^–3. В силу этого обстоятельства можно считать, что

.                              (4.4)

Уравнение (2.12) теперь имеет вид

.              (4.5)

Опуская для краткости дальнейшие достаточно не простые выкладки решения уравнения в цилиндрических координатах, запишем окончательное выражение для электромагнитной силы упора

,                                          (4.6)

если предположить , , .

Силу сопротивления движению подводной лодки можно представить в виде

,                                          (4.7)

где c_с = 0,05 – коэффициент сопротивления; v – скорость лодки; S – площадь поперечного сечения корпуса лодки.

При L = 200 м, а = 5 м, S =75 м², ,  можно получить отношение

 и F_z = 297980 H, a F_c = 46875 H.

С учетом джоулевых потерь КПД приближенно равен

,                                     (4.8)

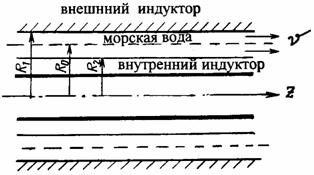
Расчеты показывают, что такая схема мало рациональна, так как приемлемый коэффициент полезного действия может быть получен только при малой скорости хода, а размеры индукторов очень велики.

Более рациональной представляется схема индукционного движителя каналового типа, представленная на рис. 4.2. В этой схеме можно получить больший КПД и большие индукции. Расчеты показывают, что при тех же габаритах лодки и скорости около 10 узлов КПД составит ок. 10%

Рис. 4.2