Глава 2.

Электромеханическое преобразование энергии

в ИМ для ВИД

 

Формула баланса энергий и мощностей в ИМ

 

ИМ – это электромеханический преобразователь энергии, осуществляющий преобразование электрической энергии, получаемой из сети, в механическую, которую он отдает в нагрузку, с обязательным выделением тепла.

 

          Этот процесс описывается уравнениями баланса энергий и мощностей, которые следуют из второго закона Кирхгофа для электрической цепи, образованной источником питания и фазной обмоткой.

 

Фаза ИМ обладает активным и изменяющимся в широком диапазоне индуктивным сопротивлениями. Второй закон Кирхгофа для фазы в общем случае имеет вид

 

u + e=iR                                                                                          (12)

где u – напряжение сети;

i–мгновенное значение тока фазы;

e – ЭДС, наведенная в фазе.

 

С учетом того, что  , напряжение

 ,                                                                                   (13)

 

где – потокосцепление обмотки.

 

Потокосцепление  является функцией двух переменных: тока i и угла поворота ротора g

 

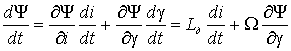 ,                                             (14)

 

где  – дифференциальная индуктивность фазы;

 – угловая частота вращения ротора;

 – трансформаторная ЭДС, обусловленная изменением тока в фазе;

 – ЭДС вращения, связанная с изменением потокосцепления фазы, которое происходит

             в результате взаимного перемещения сердечников статора и ротора.

 

Уравнение (14) представляет собой важное соотношение, показывающее, что ЭДС, наводимая в обмотках электрических машин, в общем случае складывается из двух составляющих. Одна из них обусловлена изменением тока в обмотке и не связана с перемещением сердечников; вторая – определяется приращением потокосцепления фазы в результате перемещения сердечников при условии неизменности токов возбуждающих контуров. Второе слагаемое принято называть ЭДС вращения. Характер движения, приводящий к ее возникновению может быть различным (например, возвратно–поступательное движение в линейном ВИД), поэтому данную ЭДС можно назвать ЭДС движения.

 

С учетом (14) уравнение (13) можно переписать так

 

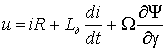 .                                                                     (15)

 

Умножая обе части последнего равенства на ток i , получим уравнение баланса мгновенных мощностей в ВИД

 

p= pэл + pмех+ pW,                                                                           (16)

 

где p=ui – мгновенная мощность, получаемая фазой двигателя от источника питания;

 

p эл=i2R – мгновенная мощность, выделяющаяся в виде тепла на активном сопротивлении фазы;

 

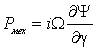– мгновенная механическая мощность;

 

 – мощность, идущая на приращение энергии запасенной в магнитном поле.

 

Таким образом, мощность, полученная фазой ВИД от источника питания, расходуется на совершение механической работы, приращение энергии магнитного поля и электрические потери.

 

Умножив левую и правую части уравнения баланса мощностей на бесконечно малую времени dt, получим уравнение баланса энергий

 

pdt =dWэл+ dWкоэн+dWмагн.                                                            (17)

 

где pdt – электрическая энергия, поступившая в фазу ИМ от источника питания за промежуток времени dt;

dWэл – электрическая энергия, выделившаяся в виде тепла в фазе ИМ за то же время;

dWкоэн+dWмагн=idΨ – часть энергии, потупившей от источника питания в ИМ за вычетом электрических потерь;

dWкоэн= pмех dt – часть энергии магнитного поля, израсходованная на совершение механической работы (коэнергия);

dWмагн= pW dt – часть энергии, полученной от источника питания и израсходованная на приращение энергии магнитного поля (энергия магнитного поля).

 

Таким образом, электрическая энергия, поступающая из источника в ИМ, расходуется на электрические потери, приращение энергии магнитного поля и совершение механической работы [2].

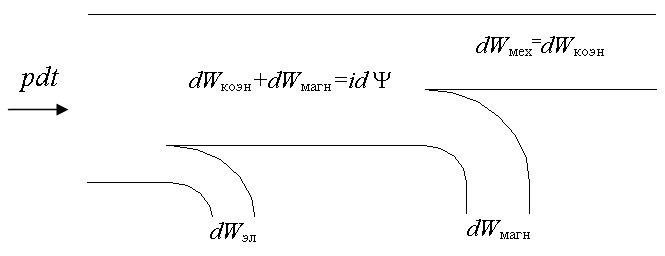
Рис. 22. Диаграмма электромеханического преобразования энергии.

 

Графическая интерпретация энергии магнитного поля и коэнергии

 

Описание процессов электромеханического преобразования энергии в ВИД принято проводить по энергетическим диаграммам, которые дают возможность визуализировать многие расчетные величины и формулы. Энергетические диаграммы строят на плоскости ().

 

Рис. 23. Энергетическая диаграмма ИМ.

 

Предположим, что в некоторый момент времени фаза ИМ имеет потокосцепление 1 и по ней протекает ток i1. На плоскости () этому моменту времени соответствует рабочая точка В(i , 1). При этом энергия, поступающая в двигатель от источника питания за вычетом электрических потерь Wкоэн+Wмагн, будет равна произведению 1·i1. На энергетической диаграмме ему соответствует площадь прямоугольника ОАВС, образованного координатными осями и параллельными им линиями, проходящими через рабочую точку.

 

Для определения энергии, запасенной в магнитном поле Wмагн, и коэнергии Wкоэн в рассматриваемый момент времени требуется знать не только координаты рабочей точки, но и предысторию магнитного состояния системы – кривую намагничивания сердечников ИМ током фазы.

 

Кривой намагничивания электропроводящего контура называется зависимость его потокосцепления от тока при постоянстве пространственного положения всех элементов магнитной системы.

 

На плоскости () существует бесконечное множество кривых намагничивания фазы ИМ, но только одна из них проходит через рабочую точку В(i1 , 1). Она делит прямоугольник ОАВС на два, в общем случае, неравных криволинейных треугольника. При этом площадь верхнего треугольника пропорциональна энергии, запасаемой в магнитном поле, а нижнего – коэнергии.

 

Последнее утверждение вытекает из следующих соображений. Предположим, что на фазу ИМ подано напряжение и по ней протекает ток, но в силу большого момента сопротивления частота вращения ротора равна нулю. Из анализа уравнения баланса энергий для данного случая следует, что энергия, поступающая от источника, расходуется на электрические потери и приращение энергии магнитного поля dWмагн, то есть

 

dWкоэн+dWмагн=dWмагн=idΨ .                                                            (18)

 

Количество энергии, запасенное в магнитном поле при изменении потокосцепления от нулевого значения до величины 1, определяется интегралом

 

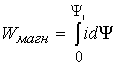,                                                                               (19)

 

который имеет геометрический смысл площади над кривой намагничивания. Таким образом, энергия, запасаемая в магнитном поле при электромеханическом преобразовании энергии, пропорциональна площади криволинейного треугольника над кривой намагничивания. Следовательно, так как суммарная энергия системы пропорциональна площади прямоугольника со сторонами i1 и 1, и равна сумме энергий Wмагн и Wкоэн, то коэнергия пропорциональна площади под кривой намагничивания.

 

Заметим, что представленная на рис. 23 энергетическая диаграмма носит дифференциальный характер, то есть она однозначно определяет энергетическое состояние системы только в одной рабочей точке. На основе совокупности таких диаграмм для большого числа рабочих точек, соответствующих полному такту коммутации фазы, можно построить энергетическую диаграмму, которая определяет энергетическое состояние системы на всем интервале коммутации. Такие диаграммы носят интегральный характер. Для их построения необходимо знать полное семейство кривых намагничивания ИМ и законы изменения координат рабочей точки.

 

Семейство кривых намагничивая фазы ИМ

 

Для построения энергетической диаграммы необходимо знать семейство кривых намагничивания ИМ. Оно может быть получено опытным путем или по результатам численного моделирования магнитного поля в ИМ.

 

Среди всех кривых намагничивания особое значение имеют кривые, соответствующие согласованному и рассогласованному положению сердечников.

 

Кривая, соответствующая рассогласованному положению сердечников (γu=0º, рис. 24), имеет линейный характер. Это объясняется относительно большим воздушным зазором между статором и ротором и, как следствие этого, ненасыщенностью магнитной системы во всем рабочем диапазоне токов. В согласованном положении (γа=22,5º, рис. 24) зазор мал и увеличение МДС катушек приводит к быстрому насыщению сердечников, после которого рост тока уже не сопровождается существенным изменением потокосцепления. Кривые, соответствующие любому другому положению ротора, занимают на плоскости (, i) промежуточное положение между описанными выше зависимостями, то есть между γu=0º и γа=22,5º для выбранной конфигурации ИМ – 12/8 (рис. 24).

 

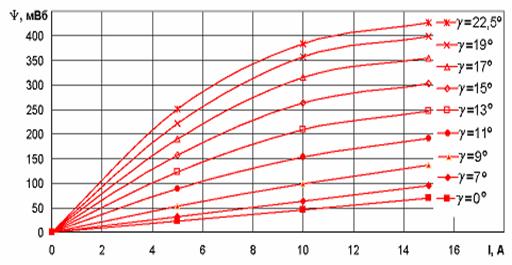
Рис. 24. Семейство кривых намагничивания ВИД конфигурации 8/6.

 

Мгновенный момент ИМ

 

Мгновенная механическая мощность, входящая в уравнение баланса мощностей (16), определяется следующим выражением

 

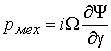.                                                                                   (20)

 

С другой стороны, любая механическая мощность определяется произведением частоты вращения ротора на электромагнитный момент

 

рмех= W×М.                                                                                       (21)

 

Сравнивая (20) и (21), можно получить выражение для мгновенного электромагнитного момента через производную потокосцепления по углу поворота ротора

 

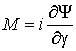 .                                                                                       (22)

 

На практике чаще используется выражение для определения электромагнитного момента через производную коэнергии. Для того, чтобы получить данное соотношение, необходимо подставить в выражение для дифференциала коэнергии

 

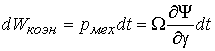.                                                             (23)

 

угловую частоту вращения

 

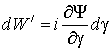  .                                                                               (24)

 

Подставляя производную , выраженную из (22), в (24), получим формулу для определения электромагнитного момента через производную коэнергии

 

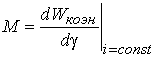 .                                                                       (25)

 

 

Таким образом, мгновенный момент ИМ может быть определен как производная коэнергии фазы по углу поворота ротора. На практике при определении мгновенного момента производную заменяют отношением приращения коэнергии при малом виртуальном перемещении ротора, осуществленном при постоянстве токов возбуждающих контуров, к величине этого перемещения.

 

Момент может быть определен и через энергию, запасенную в магнитном поле Wмагн. В этом случае его расчет следует проводить при поддержании постоянства потокосцеплений фаз двигателя.

 

Уравнение баланса энергий для случая отсутствия активного сопротивления фазы двигателя имеет вид

 

idΨ=dWкоэн+dWмагн .                                                                     (26)

 

При постоянстве потокосцепления левая часть соотношения (26) обращается в нуль. Это дает право утверждать, что в данном случае дифференциал коэнергии равен дифференциалу энергии магнитного поля с обратным знаком

 

dWкоэн= –dWмагн .                                                                         (27)

 

Так как дифференциал коэнергии равен dWкоэн=Мdγ, то выражение для момента примет вид

 

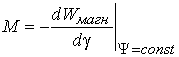.                                                              (28)

 

 

Соотношения (25) и (28) представляют собой общие уравнения метода виртуальных перемещений, который используется при определении пондеромоторных сил взаимодействия ферромагнитных тел находящихся во внешнем магнитном поле.

 

Геометрическая интерпретация этих соотношений достаточно проста. В обоих случаях момент пропорционален площади криволинейного треугольника, образованного кривыми намагничивания до и после начала виртуального перемещения и прямой, определяющей постоянное значение тока или потокосцепления, отнесенной к величине виртуального перемещения.

 

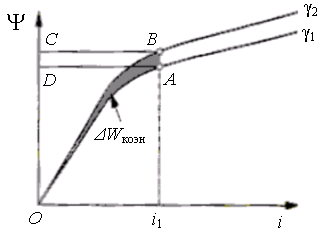
Рис. 25. К определению мгновенного момента.

 

Мгновенный момент для

линейной магнитной системы

 

В случае линейной магнитной системы энергия, запасенная в магнитном поле равна коэнергии

 

Wмагн=Wкоэн                                                                                   (29)

 

Следовательно, обе эти величины определяются как половина энергии, поступившей в двигатель от источника питания за вычетом электрических потерь.

 

.                                                                  (30)

 

С учетом того, что при линейности магнитной системы потокосцепление фазы  пропорционально ее току i, а коэффициент пропорциональности представляет собой индуктивность фазы L, соотношение (26) принимает вид

 

 .                                                                 (31)

 

Таким образом, в случае линейной магнитной системы формулы для определения мгновенного электромагнитного момента могут быть записаны следующим образом.

 

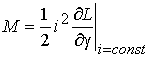                                                                        (32)

 

 

 

Из последнего соотношения вытекает, что электромеханическое преобразование энергии возможно лишь в том случае, когда имеет место изменение индуктивности фазы.

 

Индуктивность фазы ИМ

в функции углового положения ротора

 

Индуктивность фазы для линейной магнитной системы зависит только от взаимного положения сердечников, а точнее, только от проводимости зазора, которая изменяется в широких пределах на интервале от рассогласованного до согласованного положения.

 

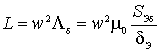                                                                        (33)

 

где L – индуктивность фазы;

w – число витков фазы;

Λδ – проводимость воздушного зазора;

μ0  – относительная магнитная проницаемость;

SЭδ – эквивалентная площадь воздушного зазора, через которую проходит магнитный поток;

δЭ – эквивалентная длина воздушного зазора.

 

На рис. 26 представлена кривая изменения индуктивности фазы ИМ в функции углового положения ротора при постоянном значении ее тока.

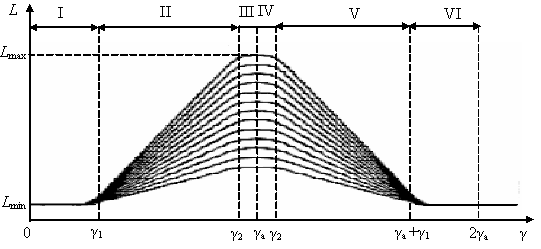
Рис. 26. Индуктивность фазы ИМ в функции углового положения ротора при различных значениях тока фазы.

 

 

На этой зависимости можно выделить несколько участков. Первый из них (участок I) характеризуется практически постоянным значением индуктивности от рассогласованного положения γu=0 до момента начала перекрытия полюсов сердечников статора и ротора γ1.

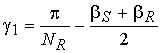 .                                                                              (34)

 

 

На этом интервале эквивалентный воздушный зазор δЭ принимает значения, близкие к максимальным. Следовательно, его проводимость будет минимальна, что и объясняет малое значение индуктивности в окрестности рассогласованного положения.

 

Начиная с углового положения, при котором происходит взаимное перекрытие полюсов статора и ротора, имеет место интенсивное возрастание эквивалентной площади SЭδ, которая пропорциональна степени перекрытия полюсов. Эквивалентный зазор при этом остается практически постоянным и имеет значение, близкое к воздушному зазору между сердечниками в согласованном положении. Таким образом, на втором участке происходит практически линейное нарастание индуктивности фазы.

 

Линейный рост индуктивности продолжается до углового положения сердечников, при котором полюса статора и ротора полностью перекрывают друг друга. В силу того, что в ИМ полюсные дуги статора и ротора выполняют не равными друг другу, полное перекрытие полюсов наступает еще до согласованного положения при угле

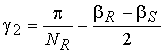                                                                             (35)

 

 

С этого углового положения сердечников начинается третий участок кривой индуктивности.

 

После полного перекрытия полюсов статора и ротора величины эквивалентного воздушного зазора и площади изменяются незначительно. Эквивалентный воздушный зазор δЭ уменьшается, а площадь SЭδ увеличивается. Их изменение обусловлено ростом потокосцепления, связанного с выпучиванием магнитного поля в область боковых поверхностей полюсов. При согласованном положении γal проводимость воздушного зазора и индуктивность фазы достигают максимально возможного в данном ВИД значения. С большой степенью точности индуктивность согласованного положения можно определить по формуле

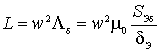,                                                                               (36)

 

где SSδ– площадь поперечного сечения зубца статора.

 

Таким образом, на интервале от γ2 до γa происходит более плавное по сравнению со вторым участком увеличение индуктивности до максимального значения.

 

Дальнейшее вращение ротора приводит к уменьшению проводимости воздушного зазора. Сначала это происходит относительно медленно, что характерно для интервала от согласованного положения до положения, при котором полюса статора и ротора выходят из зоны взаимного перекрытия (участок IV). Затем, при частичном перекрытии полюсов проводимость и индуктивность резко уменьшаются в силу уменьшения степени перекрытия полюсов (участок V). При выходе полюсов из зоны перекрытия индуктивность по аналогии с участком I остается практически постоянной и плавно уменьшается до значения индуктивности рассогласованного положения (участок VI).

 

Таким образом, кривая изменения индуктивности в зависимости от угла поворота ротора симметрична относительно согласованного положения.

 

Кривые изменения мгновенного тока и момента фазы в функции

углового положения ротора при линейной магнитной системе

 

Знание зависимости индуктивности фазы дает возможность построить кривую тока и с ее помощью по формуле (32) определить характер кривой момента.

 

Предположим, что при угловом положении сердечников γuγon<γ1 на фазу А ИМ подается постоянное напряжение U, а при угле поворота γ1γoff<γ2 оно инвертируется, как это показано на рис. 27.б.

 

Как только к фазе ИМ прикладывается напряжение, по ней начинает протекать тока. Так как напряжение подается на фазу при угловом положении, соответствующем первому участку кривой индуктивности, на котором эта величина минимальна, то на интервале от γon до γ1 происходит интенсивное нарастание тока (рис. 27.в). Производная  здесь положительна, близка к нулю. Момент, развиваемый фазой на этом интервале, носит движущий характер и представляет собой относительно малую величину.

 

Участок II кривой L=L(γ) характеризуется резким нарастанием индуктивности, в силу чего ток на этом интервале имеет убывающий характер. Производная  здесь положительна и отлична от нуля. Как следствие этого, при малом перекрытии полюсов, когда производная индуктивности уже отлична от нуля и положительна, а ток еще достаточно велик, наблюдается резкое нарастание момента, за которым следует плавное его уменьшение, вызванное убывающим характером токовой волны.

 

Инвертирование напряжения, приложенного к фазе при угле поворота ротора γoff, то есть изменение его знака, приводит к ускорению процесса спадания тока. До углового положения γ2 производная индуктивности остается положительной и отличной от нуля. Таким образом, на данном интервале фаза продолжает развивать движущий момент, который носит убывающий характер.

 

На участке III (рис. 26) кривой индуктивности эта величина медленной возрастает до своего максимального значения. Поэтому ее производная плавно уменьшается до нулевого значения в согласованном положении. Ток также продолжает уменьшаться. Это приводит к тому, что момент в согласованном положении достигает нулевого значения.

 

В том случае если до согласованного положения ток не успел уменьшиться до нуля, то в силу отрицательного значения производной индуктивности на участке IV (рис. 26) фаза ИМ будет развивать на нем тормозной момент. Последнее явление носит негативный характер и ухудшает характеристики двигателя. Поэтому стремятся подобрать углы включения и отключения таким образом, чтобы фазы ИМ не развивали тормозного момента.

 

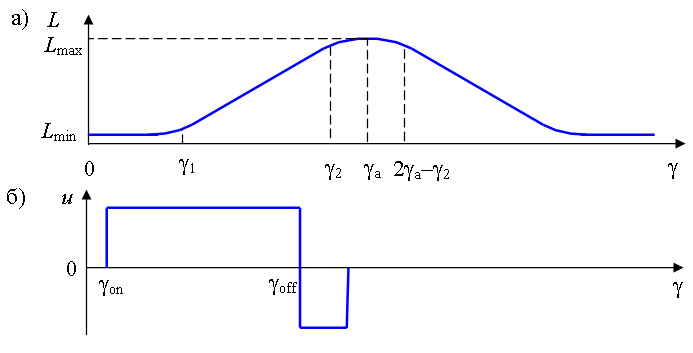
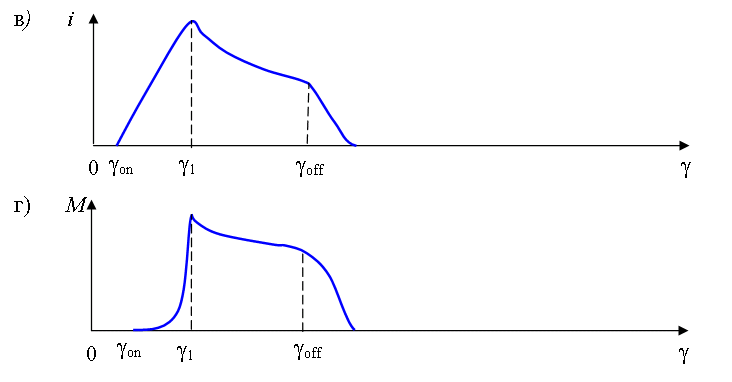
Рис. 27. К определению кривых мгновенного тока и момента фазы ИМ:

а) зависимость индуктивности фазы L=L(γ);

б) зависимость, приложенного к фазе напряжения;

в) токовая волна;

г) волна момента.

 

Энергетическая диаграмма интегрального типа

 

Зная полное семейство кривых намагничивания фазы ВИД, а также характер изменения ее тока и потокосцепления на интервале коммутации, можно построить энергетическую диаграмму для данного интервала.

 

Так как в начале и в конце такта коммутации ток и потокосцепление фазы равны нулю, то годограф движения рабочей точки на плоскости  () будет иметь вид замкнутой кривой, представленной на рис. 28.

 

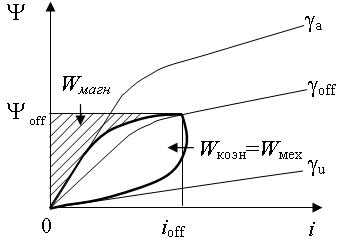
Рис. 28. Энергетическая диаграмма интервала коммутации фазы ВИД.

 

При этом площадь, охваченная годографом, представляет собой коэнергию, преобразованную фазой в механическую работу на интервале коммутации, а площадь, обозначенная на рис. 28 буквой Wмагн, пропорциональна энергии, накопленной в магнитном поле фазы и возвращенной после окончания ее работы в источник через обратные диоды.

 

Энергетическая диаграмма такта коммутации фазы ВИД дает возможность определить многие интегральные величины. 

 

Так, например, по ней легко вычислить энергетическое отношение, которое используется для характеристики эффективности электромеханического преобразования энергии в ВИД и  задается формулой

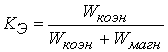.                                                                        (37)

 

 

В ненасыщенной машине это отношение в принципе не может быть больше 0.5, что следует из рассмотрения энергетических диаграмм. В случае насыщения магнитной системы двигателя эффективность преобразования повышается, и коэффициент KЭ растет.

 

Позволяет годограф определить и средний момент ВИД. Он может быть рассчитан по формуле

,                                                                           (38)

 

где m–число фаз двигателя;

NR-число полюсов ротора.

 

Контрольные вопросы и упражнения

 

1. Запишите уравнения баланса энергий и мощностей в ИМ и поясните их физический смысл.

2. Что такое энергетическая диаграмма?  Какие типы энергетических диаграмм Вы знаете? Чем они отличаются?

3. Что такое коэнергия? Поясните графический смысл этой величины.

4. Выведите формулы для вычисления мгновенного электромагнитного момента по изменению энергии магнитного поля и коэнергии. Поясните их графический смысл.

5. Опишите характер зависимостей индуктивности и тока фазы, мгновенного момента.

6. Почему индуктивность фазы ИМ в рассогласованном положении всегда отлична от нуля?

7. Что такое энергетическое отношение? Как оно вычисляется? Поясните графический смысл этой величины.

8. Почему энергетическое отношение в ненасыщенной ИМ всегда равно 0,5?

9. Для ИМ, конфигурации которых приведены в Приложении 1, определите индуктивность фазы в согласованном и рассогласованном положении. Все машины имеют воздушный зазор δ=0,3 мм, число витков фазной катушки wk=50, длина сердечников l=100 мм, ширина полюсов статора и ротора b=15 мм, отношение максимальной к минимальной индуктивности фазы равно 7. Катушки фазы включены в электрическом отношении последовательно, в магнитном – согласно. Магнитная система двигателей в согласованном положении ненасыщена.