Глава
3
Методика
расчета семейства кривых намагничивания фазы ИМ
Расчет магнитной
цепи ИМ предполагает определение семейства кривых намагничивания фазы ![]() с
некоторым шагом по угловому положению ротора γ. При этом, чем большее
число кривых намагничивания определено при расчете магнитной цепи, тем точнее
будут результаты расчета других характеристик двигателя.
с
некоторым шагом по угловому положению ротора γ. При этом, чем большее
число кривых намагничивания определено при расчете магнитной цепи, тем точнее
будут результаты расчета других характеристик двигателя.
Среди бесконечно
большого числа кривых намагничивания особое место занимают кривые, соответствующие
согласованному ![]() =
=![]() a и рассогласованному
положению фазы
a и рассогласованному
положению фазы ![]() =
=![]() u. Следует отметить, что все
остальные кривые на плоскости
u. Следует отметить, что все
остальные кривые на плоскости ![]() располагаются
между ними. Поэтому расчет магнитной цепи двигателя необходимо начинать именно
с определения этих зависимостей.
располагаются
между ними. Поэтому расчет магнитной цепи двигателя необходимо начинать именно
с определения этих зависимостей.
Расчеты
показывают, что для определения кривых намагничивания очень удобно пользоваться
зависимостями ![]() . Найдя аналитические выражения для них,
достаточно просто перейти к кривым намагничивания. Именно такой подход
реализован в методике, описанной ниже [1].
. Найдя аналитические выражения для них,
достаточно просто перейти к кривым намагничивания. Именно такой подход
реализован в методике, описанной ниже [1].
Кривая
намагничивания согласованного положения
Кривая
намагничивания в согласованном положении имеет два ярко выраженных участка.
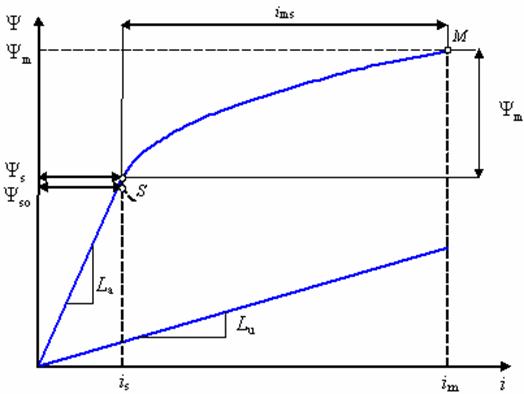
Рис. 29.
Аппроксимация кривой намагничивания в согласованном и рассогласованном
положении.
На первом
участке магнитная система ненасыщена и ферромагнитные
части имеют магнитную проницаемость близкую к бесконечности. Следовательно, их
магнитное сопротивление протеканию потока равно нулю. Таким образом, на этом
участке кривой намагничивания вся МДС фазы приложена только к сопротивлению,
обусловленному наличием в магнитной системе воздушных зазоров. Функция,
описывающая кривую намагничивания, в данном случае имеет вид
![]() ,
(39)
,
(39)
где ![]() – линейная
индуктивность согласованного положения.
– линейная
индуктивность согласованного положения.
Величина ![]() имеет
очень важное значение для проведения дальнейшего
расчета магнитной системы и может быть определена как по результатам численного
моделирования магнитного поля в машине, так и аналитически
имеет
очень важное значение для проведения дальнейшего
расчета магнитной системы и может быть определена как по результатам численного
моделирования магнитного поля в машине, так и аналитически
![]()
![]()
![]() 0
0![]() (40)
(40)
где w –
число витков фазы;
![]() –проводимость воздушного зазора в согласованном положении;
–проводимость воздушного зазора в согласованном положении;
Sp –
площадь поперечного сечения зубца статора;
![]() – воздушный зазор.
– воздушный зазор.
На втором
участке кривой намагничивания происходит постепенное насыщение магнитной
системы, в результате которого магнитная проницаемость стали снижается, что
приводит к существенному росту ее магнитного сопротивления. Особо следует
отметить, что данный рост носит нелинейный характер. Данный участок кривой
намагничивания носит название нелинейного участка. Кривая намагничивания здесь
аппроксимируется квадратичной функцией, параметры которой должны быть подобраны
таким образом, чтобы не было разрывов первой производной на границе участков
(при токе ![]() ) и чтобы полученная в результате аналитического
расчета кривая проходила через точку (
) и чтобы полученная в результате аналитического
расчета кривая проходила через точку (![]() ), которая определяется по результатам
полевого расчета. Исходя из этого
), которая определяется по результатам
полевого расчета. Исходя из этого
![]() 2
2![]() ,
(41)
,
(41)
где ![]() ,
, ![]() – параметры,
обеспечивающие неразрывность первой производной кривой намагничивания при токе
– параметры,
обеспечивающие неразрывность первой производной кривой намагничивания при токе ![]() ;
;
а – параметр, который определяется исходя из условия
прохождения кривой намагничивания через точку (![]() ).
).
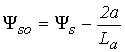 (42)
(42)
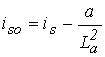 (43)
(43)
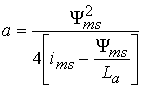 (44)
(44)
где ![]() ,
(45)
,
(45)
![]() .
(46)
.
(46)
Для
полного определения кривой намагничивания согласованного положения необходимо
найти аналитическое выражение для вычисления тока, при котором происходит
переход с линейного на нелинейный участок характеристики. Если известна
индукция насыщения стали ![]() , то
, то ![]() определяется как ток, при котором индукция в
воздушном зазоре равна индукции насыщения стали, то есть
определяется как ток, при котором индукция в
воздушном зазоре равна индукции насыщения стали, то есть
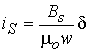 (47)
(47)
Геометрический
смысл параметров аппроксимирующих функций поясняется рис. 29.
Таким образом,
описанная выше методика позволяет провести аналитический расчет кривой
намагничивания согласованного положения по результатам только одного полевого
расчета при токе ![]() . Все остальные коэффициенты аппроксимирующих
функций определяются аналитически.
. Все остальные коэффициенты аппроксимирующих
функций определяются аналитически.
Кривая
намагничивания рассогласованного положения
Анализ кривых
намагничивания рассогласованного положения (рис. 24), показывает, что эти
зависимости в рабочей области токов имеют линейный характер. Это объясняется
достаточно большим по сравнению с согласованным положением воздушным зазором и,
как следствие этого, его высоким магнитным сопротивлением. В рассогласованном
положении практически невозможно достичь насыщения магнитной системы, поэтому
кривая намагничивания описывается линейной функцией
![]() ,
(48)
,
(48)
где
![]() –
индуктивность рассогласованного положения фазы.
–
индуктивность рассогласованного положения фазы.
Данная
величина является единственным параметром, знание которого необходимо для
определения кривой намагничивания рассогласованного положения. Индуктивность
рассогласованного положения, как правило, определяется по результатам полевого
расчета.
Методика расчета характеристик ![]()
На
рис.30 представлены зависимости ![]()
![]() , полученные путем расчета
магнитного поля в различных двигателях. Проанализируем их.
, полученные путем расчета
магнитного поля в различных двигателях. Проанализируем их.
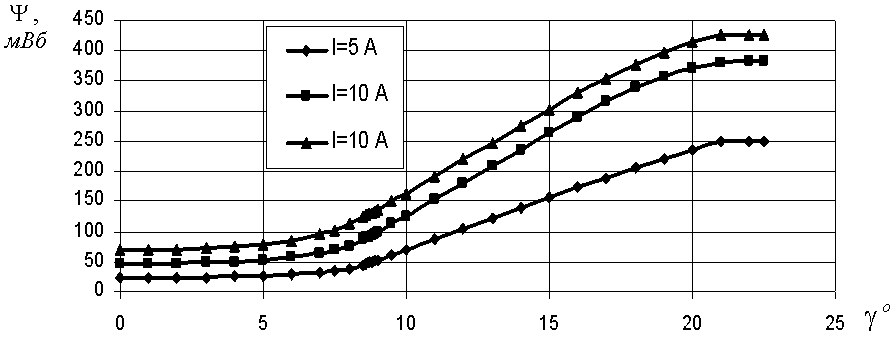
Рис.
30. Зависимости ![]() для ИМ конфигурации 8/6 (а) и 12/8
(б).
для ИМ конфигурации 8/6 (а) и 12/8
(б).
Зависимости
рис. 30 имеют возрастающий характер. Рост потокосцепления фазы при изменении
угловой координаты ротора от рассогласованного к согласованному положению при
постоянстве тока объясняется ростом магнитной проводимости воздушного зазора.
Следует отметить, что потокосцепление фазы в рассогласованном положении линейно
возрастает с ростом тока, в то время как в согласованном положении потокосцепление
фазы увеличивается нелинейно с ростом тока, что полностью соответствует
сделанным ранее выводам.
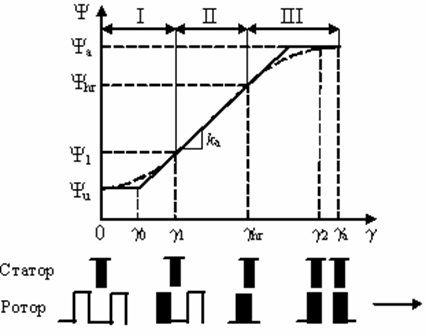
Рис.
31. Участки зависимости ![]() .
.
Зависимости
![]() имеют три
четко выраженных участка. На первом (
имеют три
четко выраженных участка. На первом (![]() ) потокосцепление фазы остается практически неизменным
при варьировании угловой координаты. На втором (
) потокосцепление фазы остается практически неизменным
при варьировании угловой координаты. На втором (![]() ) наблюдается линейный рост
потокосцепления с увеличением угла. Третьему участку (
) наблюдается линейный рост
потокосцепления с увеличением угла. Третьему участку (![]() ) соответствует плавное нарастание потокосцепления
до значения соответствующего потокосцеплению согласованного положения.
) соответствует плавное нарастание потокосцепления
до значения соответствующего потокосцеплению согласованного положения.
Граничные
углы (![]() ,
,![]() ,
,![]() ) могут быть определены следующим
образом:
) могут быть определены следующим
образом:
–
угол соответствующий согласованному положению
![]() ,
(49)
,
(49)
–
угол соответствующий началу перекрытия полюсов статора
и ротора
![]() ,
(50)
,
(50)
где
![]() – полюсная дуга статора;
– полюсная дуга статора;
![]() – полюсная дуга ротора.
– полюсная дуга ротора.
–
угол ![]() определяется, как
определяется, как
![]() (51)
(51)
где
![]() – угол,
соответствующий началу полного перекрытия полюсов.
– угол,
соответствующий началу полного перекрытия полюсов.
По
аналогии с определением кривых намагничивания для согласованного положения,
расчет зависимостей ![]() следует проводить по отдельным
участкам. При этом лучше всего начинать со второго участка, как с наиболее
простого.
следует проводить по отдельным
участкам. При этом лучше всего начинать со второго участка, как с наиболее
простого.
Расчет кривой ![]() на втором
участке
на втором
участке ![]()
Так как на втором участке зависимость 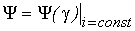 имеет линейный
характер, то она может быть аппроксимирована функцией
имеет линейный
характер, то она может быть аппроксимирована функцией
![]() ,
(52)
,
(52)
где ![]() – потокосцепление рассогласованного положения при данном
токе;
– потокосцепление рассогласованного положения при данном
токе;
![]() – угол, который определяется как точка пересечения горизонтальной
прямой, соответствующей потокосцеплению рассогласованного положения
– угол, который определяется как точка пересечения горизонтальной
прямой, соответствующей потокосцеплению рассогласованного положения ![]() , и продолжения прямолинейного участка зависимости
, и продолжения прямолинейного участка зависимости ![]() ;
;
![]() – тангенс угла наклона
прямолинейного участка зависимости
– тангенс угла наклона
прямолинейного участка зависимости ![]()
Для определения 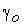 может быть
использована эмпирическая формула
может быть
использована эмпирическая формула
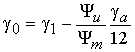 (53)
(53)
Коэффициент ![]() определяется как
определяется как
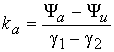 (54)
(54)
Следует особо отметить, что тангенс угла
наклона зависимости потокосцепления фазы от углового положения ротора
при постоянном токе ![]() и угол
и угол ![]() будут иметь различное
значение для различных уровней тока.
будут иметь различное
значение для различных уровней тока.
Расчет кривой ![]() на первом
участке
на первом
участке ![]()
На первом
участке зависимость ![]() имеет
нелинейный характер и моделируется при помощи Fröhlich
аппроксимации
имеет
нелинейный характер и моделируется при помощи Fröhlich
аппроксимации
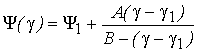 ,
(55)
,
(55)
где ![]() – потокосцепление в точке
– потокосцепление в точке ![]() , величина которого определяется по формуле для
второго участка;
, величина которого определяется по формуле для
второго участка;
A, B – коэффициенты,
определяемые исходя из условий, что при рассогласованном положении
потокосцепление, рассчитанное по данной формуле, должно быть равно величине,
определенной по кривой намагничивания для рассогласованного положения, то есть ![]() ; и что в конце первого участка производная
потокосцепления по угловой координате должна быть равна тангенсу угла наклона
характеристики
; и что в конце первого участка производная
потокосцепления по угловой координате должна быть равна тангенсу угла наклона
характеристики ![]() на втором
участке, то есть
на втором
участке, то есть 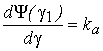 .
.
Исходя из необходимости
выполнения этих условий, коэффициенты A, B могут быть определены
следующим образом
A=![]() В, (56)
В, (56)
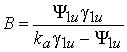 ,
(57)
,
(57)
где ![]() , (58)
, (58)
![]() .
(59)
.
(59)
Расчет кривой ![]() на
третьем участке
на
третьем участке ![]()
Как
и на первом участке, на третьем зависимость ![]() моделируется при помощи Fröhlich аппроксимации
моделируется при помощи Fröhlich аппроксимации
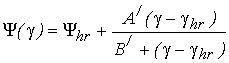 (60)
(60)
где ![]() – потокосцепление в точке
– потокосцепление в точке ![]() , величина которого определяется по формуле для второго
участка;
, величина которого определяется по формуле для второго
участка;
A/, B/ – коэффициенты, определяемые исходя из условий, что
при согласованном положении потокосцепление, рассчитанное по данной формуле, должно
быть равно величине, определенной по кривой намагничивания для согласованного
положения, то есть ![]() ; и что в начале третьего участка производная потокосцепления
по углу поворота ротора должна быть равна тангенсу угла наклона характеристики
; и что в начале третьего участка производная потокосцепления
по углу поворота ротора должна быть равна тангенсу угла наклона характеристики ![]() на втором
участке, то есть
на втором
участке, то есть 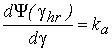 .
.
Исходя из необходимости
выполнения этих условий, коэффициенты A/, B/ могут быть определены следующим образом
A/=![]() В/
, (61)
В/
, (61)
В/=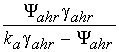 ,
(62)
,
(62)
где ![]() ,
(63)
,
(63)
![]() .
(64)
.
(64)
Таким образом,
полученные выше зависимости позволяют построить кривую потокосцепления фазы в
функции углового положения ротора при постоянном значении тока. При этом
исходными данными являются геометрические размеры и значения потокосцепления
фазы для согласованного и рассогласованного положения при заданном уровне тока.
Методика расчета кривых намагничивания
при произвольном угловом
положении сердечников статора и ротора
Кривая
намагничивания представляет собой зависимость потокосцепления фазы от тока при
постоянном угловом положении ротора. Выше была описана методика расчета
зависимостей изменения фазного потокосцепления в функции углового положения
ротора при постоянном значении тока. Таким образом, расчет кривой
намагничивания при произвольном положении сердечников может быть сведен к
расчету кривых ![]() при
данном значении угла
при
данном значении угла ![]() и различных
значениях тока i.
и различных
значениях тока i.
Зависимости ![]() имеют три
участка. Следовательно, на плоскости
имеют три
участка. Следовательно, на плоскости ![]() можно выделить кривые
намагничивания трех типов, каждый из которых соответствует определенному выше
диапазону изменения угла
можно выделить кривые
намагничивания трех типов, каждый из которых соответствует определенному выше
диапазону изменения угла ![]() . На рис. 32 показаны области существования кривых
намагничивания различных типов. Ниже приводятся алгоритмы расчета кривых
намагничивания для них.
. На рис. 32 показаны области существования кривых
намагничивания различных типов. Ниже приводятся алгоритмы расчета кривых
намагничивания для них.
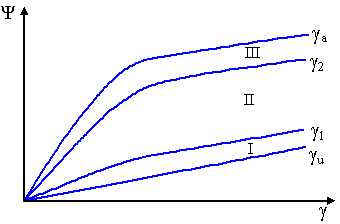
Рис. 32.
Кривые намагничивания при различных взаимных положениях статора и ротора.
Алгоритм
расчета кривых намагничивания в области II (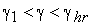 )
)
Расчет кривых намагничивания
в данной области проводится в соответствии с уравнением (52), которое с учетом
(41), (42), (43) и (48) может быть записано в виде
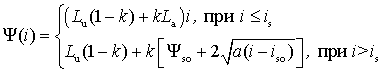 , (65)
, (65)
где 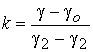 (66)
(66)
Следует
заметить, что угол ![]() будет различным
для различных значений тока. Для каждого конкретного случая его следует
определять по формуле (48).
будет различным
для различных значений тока. Для каждого конкретного случая его следует
определять по формуле (48).
Таким образом,
в области II можно определить любую кривую намагничивания по
достаточно простым формулам.
Алгоритм расчета кривых намагничивания в области I (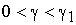 )
)
Алгоритм
расчета кривой намагничивания в области I сводится к циклическому
расчету потокосцепления по формуле (50) при различных значениях тока. При этом
последовательность расчета кривой намагничивания при некотором угловом
положении ротора ![]() может быть
представлена следующим образом.
может быть
представлена следующим образом.
Шаг 1. Установка тока на минимальном
уровне.
Шаг 2. Определение коэффициентов А и В формулы (55) для текущего значения тока по формулам (56-59).
Шаг 3. Расчет потокосцепления по формуле (55).
Шаг 4. Приращение по току.
Шаг 5. Если текущее значение тока меньше максимального, то
возврат на шаг 2, иначе выход из цикла.
Алгоритм расчета кривых намагничивания в области III (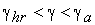 )
)
Алгоритм
расчета кривой намагничивания в области III ничем не отличается от алгоритма
расчета кривых намагничивания в первой области с той лишь разницей, что потокосцепление
определяется не по формуле (55), а по формуле (60).
Контрольные
вопросы и упражнения
1. Опишите методику расчета кривых
намагничивания в согласованном и рассогласованном положении.
2. Опишите методику расчета
кривых ![]() .
.
3. Опишите алгоритмы расчета
кривых намагничивания в областях I, II и III.
4. Реализуйте методику
расчета кривых намагничивания в программном пакете по Вашему выбору.