Глава 4
Пондеромоторные силы,
действующие на зубцы ИМ
Пульсации момента являются одним из главных
особенностей и недостатков ИМ и ВИД. Пути их уменьшения могут быть найдены
только на основе четкого представления механизмов
электромагнитного взаимодействия сердечников статора и ротора.
Исследование природы электромагнитного
момента и пондеромоторных сил (ПС), порождающих его,
принято проводить с использованием численных методов моделирования магнитного
поля и специальных расчетных моделей.
Магнитная связь между фазами ИМ с
диаметральным расположением фазных катушек пренебрежимо мала, что позволяет
представить ИМ в виде совокупности NS/2 клапанных реле и рассматривать процессы,
происходящие в них, независимо. Момент в них возникает как результат
появления азимутальных (или тангенциальных) сил взаимодействия между парой
зубцов, одного на статоре, другого на роторе, причем катушка с током размещена
на зубце статора [4–5].
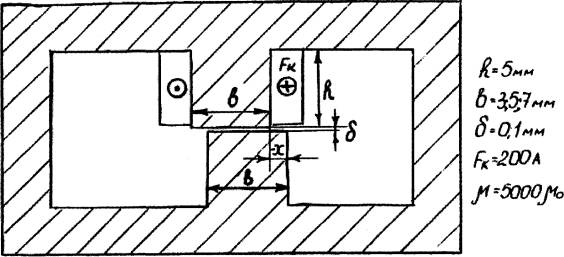
Рис.
33. Зона двух зубцов ИМ при особых граничных условиях.
Полностью автономное взаимодействие двух
таких зубцов должно быть исследовано при особых граничных условиях [5], т.е.
при отсутствии обратного магнитного потока.
Для расчета ПС существует три метода:
– метод виртуальных перемещений по
изменению энергии или коэнергии при малом перемещении;
– по натяжениям в магнитном поле;
– по формуле Лоренца по
объемной и поверхностной плотностям ЭМС в магнитном поле.
Базовым для определения ЭМС является
энергетический метод, описанный в Главе 2. При определении ПС по методу
натяжений, в отличие от энергетического метода, можно ограничиться однократным
расчетом, что обусловило популярность этого метода при применении ЭВМ.
Выражение для натяжения 
на произвольно ориентированной в магнитном поле
поверхности в векторной форме имеет вид [3], стр.140
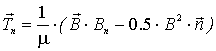(67)
где 
– вектор индукции в
рассматриваемой точке поверхности;
– магнитная
проницаемость среды в этой точке;
– нормальный
орт к той стороне поверхности, на которую действует натяжение 
;
Вn – нормальная составляющая вектора
индукции.
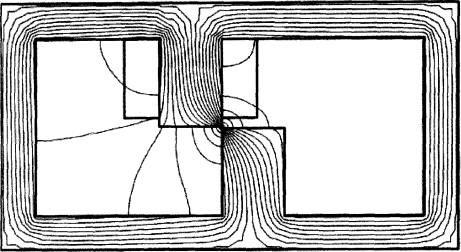
Рис. 34.
Картина магнитного поля зоны двух зубцов при особых граничных условиях.
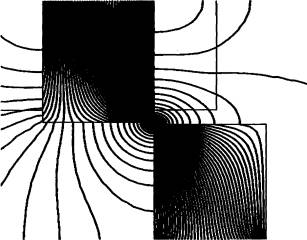
Рис.
35. Фрагмент магнитного поля зоны двух зубцов.
Аналитически нахождение
усилий между зубцами может быть получено только в предположении бесконечной
магнитной проницаемости ферромагнитных сред. С учетом нелинейностей материалов
достоверными являются только численные методы.
На рис. 34 и рис. 35 приведены картины
магнитного поля для модели рис. 33, полученные с использованием метода конечных
элементов. Для этой модели была проведена серия расчетов магнитного поля и
определены особенности поведения азимутальных сил, действующих на боковые
стороны зубцов (рис. 36).
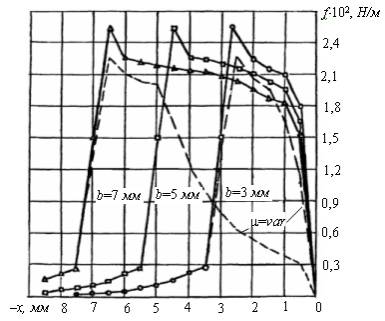
Рис. 36. Тангенциальное усилия на зубец
в зависимости от смещения при постоянной
магнитной проницаемости зубцов и их переменной ширине.
Как очевидно, безразлично
по каким боковым поверхностям зубцов проводить интегрирование натяжений по
(67): по роторным или статорным. Результат будет одинаковым. Расчет натяжений проводился для
магнитных сред с постоянной, достаточно большой относительной проницаемостью
порядка нескольких тысяч. Тангенциальные усилия, определенные для зубцов
различной ширины, обнаруживают при больших значениях 
одинаковую
особенность. При постоянной магнитной проницаемости зубцов кривые возрастания
тангенциального усилия f при сближении зубцов (уменьшении
абсолютного значения x) имеют практически одинаковый наклон при
различной ширине зубцов b. Этот эффект вполне объясним, т.к.
тангенциальное усилие при приближении угла одного зубца к углу другого при
постоянной МДС возбуждающей поле катушки определяется только магнитным полем
между приближающимися кромками (рис. 35) и не зависит от общей ширины зубцов,
если она не слишком мала.
При небольшом взаимном перекрытии зубцов (|x|<b) наблюдается максимальное значение усилия.
В этом положении имеет место только локальное насыщение углов зубцов, общее же
насыщение незначительно. При значительных перекрытиях (малых |x|) тангенциальное усилие постепенно снижается, т.к. начинает сказываться
общее насыщение зубцов и МДС, приходящаяся на зазор, уменьшается.
Максимальное значение тангенциального
усилия на единицу длины сердечника может быть рассчитано по формулам
;
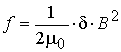(68)
,
(69)
где В – индукция в зазоре при продольном положении зубца ротора при МДС Fδ, приходящейся на зазор.
Выразив f в
относительной форме смещения зубцов можно перестроить кривые тангенциальных
усилий в обобщенном виде (рис. 37).
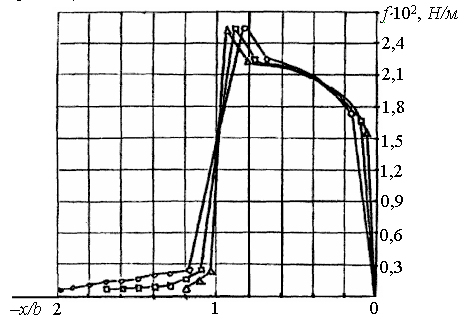
Рис.
37. Тангенциальные усилия на зубец в функции относительного смещения.
Кривые тангенциальных усилий состоят из
трех участков:
а) зоны нарастания усилий, более или менее
одинаковых для любой ширины зубцов, когда происходит сближение
взаимодействующих кромок зубцов; при небольшом взаимном перекрытии наблюдается
малообъяснимый пик усилий, определяемый, возможно, чрезвычайно сильным
насыщением сближающихся углов зубцов;
б) зоны более или менее постоянного усилия,
наличие которой хорошо объясняется с энергетических позиций. При заметном взаимном
перекрытии (уменьшении |x|) изменение энергии катушки происходит с
постоянным градиентом, зависящим от практически постоянной индукции и зазора;
в) зоны спадания усилия, когда оси зубцов
близки к совпадению.
Изменение зазора приводит к практически обратно
пропорциональному изменению усилий (рис. 38).
Рис.
38. Тангенциальные усилия в функции смещения зубцов
при
различных величинах воздушного зазора и постоянной
МДС.
Исследование усилий для нелинейных сред (
) показало, что максимальное усилие в довольно
слабой степени зависит от нелинейности сталей и сохраняет квадратичную
зависимость от МДС зазора. Для сравнения на рис. 36 штриховой линией нанесена
кривая усилий при 
для двух значений ширины зубцов 3 и 7 мм. Снижение индукции
происходит в пределах 10%, усилия – (10+20%). Это обстоятельство побуждает к использованию
в ВИД высоких значений линейных нагрузок, обеспечивающих достижение больших
моментов из-за возрастания тангенциальных сил при взаимодействии сближающихся
углов зубцов. Из рис. 36 видно, что узкие зубцы предпочтительнее широких, т.к.
общее насыщение в большой степени сказывается на усилиях в широких зубцах.
Кривые усилий на рис. 36,
37, 38 были найдены при постоянной МДС катушки, возбуждающей магнитное поле
между двумя зубцами. Для
нахождения среднего усилия кривую усилий при
постоянной МДС необходимо умножить на квадрат текущего значения тока катушки
(рис. 39).
Все величины целесообразно представить в относительной форме. Получившуюся кривую относительного момента интегрируем, получая отношение среднего момента к его максимальному значению. При фазном регулировании для разных реальных форм тока это отношение колеблется в пределах от 0.25–0.28 (рис. 40).
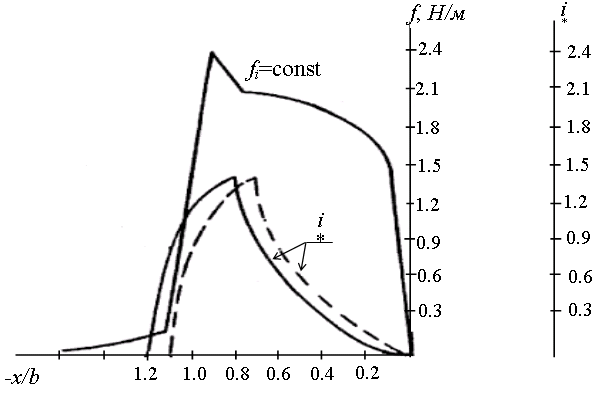
Рис. 39. Кривые тока статора (
) и тангенциальные усилия на зубец в зависимости от
относительной координаты.
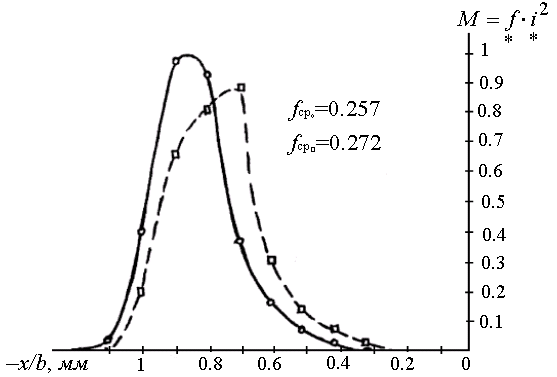
Рис. 40. Относительный момент на зубец ИМ при переменной величине тока статора.
Контрольные вопросы и упражнения
1. Опишите модель для исследования ПС в ИМ?
2. Какие методы для расчета ПС Вам известны? Как они реализуются?
3. В согласованном положении зубцов статора и ротора фазы А ИМ в воздушный зазор между ними в аксиальном направлении вводится пластина, ширина которой равна ширине полюсов, а длина – длине магнитопровода двигателя. По фазе А при этом протекает постоянный ток I. Качественно постройте зависимость аксиальной составляющей ПС, действующей на пластину при ее перемещении из бесконечности в положение, при котором она полностью находится между полюсами ИМ. При решении задачи рассмотрите три случая:
а) пластина выполнена из немагнитного материала,
б) пластина выполнена из магнитного материала с постоянной достаточно большой магнитной проницаемостью,
в) пластина выполнена из магнитного материала с магнитной проницаемостью, имеющей нелинейный характер (сталь).