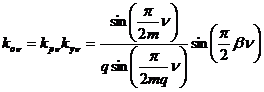Содержание

Часть 1

1.1

1.2

1.3

1.4

Часть 2

2.1

2.2

2.3

2.4

Часть 3

3.1

3.2

3.3

3.4

3.5

3.6

3.7

Литература

 Кафедра ЭМ

Применение полевых методов в электромагнитных расчетах электрических машин

1.1. Определение обмоточных коэффициентов

  (1     2     3 )

Как известно, обмоточный коэффициент ν-й гармонической k_оν входит в выражение для ЭДС и учитывает распределение обмотки по пазам и укорочение шага обмотки.

                                  (1.2)

 

Вычисление ЭДС по известной амплитуде B_ν индукции в зазоре с помощью только этих коэффициентов предполагает: 1) весь поток ν-й гармонической является потоком взаимоиндукции; 2) свойства стали сердечника, на котором расположена обмотка, не влияют на распределение поля ν-й гармонической за границами зазора и потокосцепление обмотки может быть вычислено в предположении, что магнитная проницаемость стали равна бесконечности; 3) раскрытия пазов бесконечно малы; 4) зазор в сравнении с полюсным делением мал и затухание поля ν-й гармонической в зазоре отсутствует.

Обмоточный коэффициент входит также в выражение для амплитуды МДС ν-й гармонической:

где I – действующее значение тока фазы, p – число пар полюсов машины.

Если поле в зазоре создается МДС F_νm при перечисленных выше условиях, то пространственное распределение индукции повторяет пространственное распределение МДС.

В соответствии с выражениями (1.1) и (1.3) обмоточные коэффициенты k_оν , k_рν и k_уν  могут быть определены по двум различным полевым моделям. Проиллюстрировать эти модели с помощью рисунка, не искажая при этом существенно соотношения размеров, затруднительно, поэтому приведем их подробное словесное описание.

Область задачи в обоих случаях представляет собой узкую длинную прямоугольную полосу с размерами δ, 2τ. На верхней и нижней границах области, заданы условия Неймана для векторного магнитного потенциала, на боковых границах – периодические условия.

       Для первой модели (определение k_оν по (1.1)) вблизи нижней границы формируется тонкий токовый слой, воспроизводящий гармоническое возбуждение нижнего сердечника. Как показывает опыт, для воспроизведения синусоидального распределения индукции в зазоре период гармоники достаточно (и удобно) разбить на сравнительно небольшое (18 или 24) число участков с постоянной плотностью тока на каждом. Можно также задать гармоническое возбуждение сердечника на гораздо большем числе участков, воспользовавшись средствами программирования (для пакета FEMM – на языке Lua).

Рис. 1.1 Конечно-элементная модель области воздушного зазора при гладких сердечниках

    Обмотка, для которой определяется обмоточный коэффициент, воспроизводится на модели точками, соответствующими сечениям бесконечно тонких катушечных сторон. (точки 1,2,...на рис 1.1) Располагаются точки на верхней границе (на поверхности верхнего сердечника). ЭДС катушек и всей обмотки находятся по значениям векторных потенциалов в этих точках.

       На второй модели (определение k_оν по (1.3)) обмотка задается так же, как на первой - точками, соответствующими сечениям катушечных сторон, но в этом случае в точках задаются значения соответствующих токов. Нижний сердечник не возбужден.

   Назад   Продолжение