|
|
Применение полевых методов в электромагнитных расчетах электрических машин1.1. Определение обмоточных коэффициентов
Рис. 1.2(а) Модель катушки с диаметральным шагом
Рис. 1.2(б) Модель фазы распределенной обмотки с диаметральным шагом
Рис. 1.2(в) Модель фазы распределенной обмотки с укороченным шагом
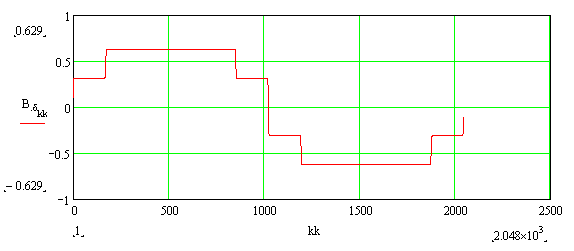
Поскольку обмоточный коэффициент на второй модели находится как отношение амплитуды ν-й гармоники индукции поля, созданного обмоткой с заданным распределением и укорочением шага, к амплитуде ν-й гармоники индукции поля сосредоточенной обмотки, для второй модели необходимо выполнить гармонический анализ поля в зазоре. Определение обмоточного коэффициента с помощью двух описанных моделей, в наибольшей мере удовлетворяющих допущениям, принятым при выводе аналитических выражений для kрν и kуν , приводит, естественно, к результатам, практически совпадающим с расчетом по этим выражениям. Приведем в качестве примера результаты моделирования при таких данных моделей: зазор – 1 мм, период (два полюсных деления) – 360 мм, толщина токового слоя вблизи поверхности нижнего сердечника (для модели первого типа) – 0,1 мм, число участков с постоянной плотностью тока в слое – 24, число узлов – 16890. Задание возбуждения сердечника с помощью токового слоя из 24 участков, кусочно аппроксимирующего гармоническое распределение линейной плотности тока iz = Iz.mcos((π/τ)x), обеспечивает практически синусоидальное распределение индукции вдоль контура, проведенного на середине высоты зазора:
Коэффициент
распределения, для обмотки с числом пазов на полюс и фазу
q
= 2, определенный на модели первого типа, равен 0,966, что менее чем на 0,01%
отличается от значения, рассчитанного по аналитической формуле (0,966). С такой
же высокой точностью совпадают с расчетными значениями определенные на модели
второго типа значения коэффициента распределения (0,966) и обмоточный
коэффициент при укорочении шага обмотки на одно зубцовое деление (0,933,
расхождение – 0,016%). Важно подчеркнуть, что обе модели вполне универсальны в том смысле, что с их помощью может быть найден обмоточный коэффициент любой обмотки, выполненной по любой схеме, с любым распределением эффективных проводников по катушкам.
Рис. 1.3. Распределение индукции вдоль средней линии воздушного зазора для обмотки с q = 2 и укорочением шага на одно зубцовое деление
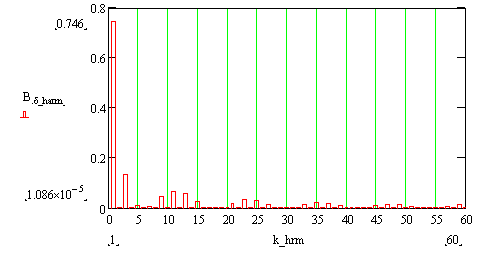
Рис. 1.4. Спектральный состав поля в зазоре для
распределенной обмотки
|