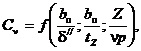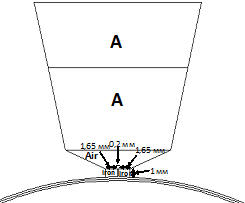
Содержание

Часть 1

1.1

1.2

1.3

1.4

Часть 2

2.1

2.2

2.3

2.4

Часть 3

3.1

3.2

3.3

3.4

3.5

3.6

3.7

Литература

 Кафедра ЭМ

Применение полевых методов в электромагнитных расчетах электрических машин

1.2. Определение коэффициента влияния пазов Сv

( 1     2 )

Возможность исследовать распределение поля в зазоре, полученное на конечно-элементной модели, с помощью гармонического анализа позволяет оценить влияние отклонения от идеализированных условий на точность расчета других коэффициентов, используемых при определении амплитуд гармоник индукции, в частности, коэффициентов влияния пазов, формулы для которых впервые получены Т.Г. Сорокером ([1-3], приведены в [1-4]).

Модель, с помощью которой оценивается влияние раскрытий пазов на амплитуды гармоник индукции, отличается от исходной (рис. 1.5) тем, что очень малые раскрытия (0,2 мм в конкретном примере) заменены более широкими (3,5 мм, см. 1.6). Для этого в модели по рис. 1.5, были предусмотрены прямоугольные участки на краях коронок зубцов, магнитная проницаемость которых при моделировании малых раскрытий задавалась большой (µ_r = 10⁴), а при моделировании больших раскрытий – равной магнитной проницаемости воздуха (µ_r = 1).

Рис. 1.6 Изменение размеров раскрытия паза на конечно-элементной модели, показанной на рис. 1.3. air – воздух, iron – сталь

По определению коэффициент влияния  пазов  равен отношению амплитуды индукции ν-й гармоники, найденной с учетом пазов, к амплитуде индукции той же гармоники при бесконечно узких пазах ([1-4]).

                                                              (1.4)

При регулярной зубчатости коэффициент влияния пазов получается одинаковым для всех зубцовых делений магнитопровода и зависит только от соотношений размеров и порядка гармонической,

                                                        (1.5)

где z - число зубцов магнитопровода; р - число периодов основной гармонической; -ширина паза у зазора.

Формулы для расчета   приведены в [1-4].

  Назад   Продолжение