Содержание

Часть 1

1.1

1.2

1.3

1.4

Часть 2

2.1

2.2

2.3

2.4

Часть 3

3.1

3.2

3.3

3.4

3.5

3.6

3.7

Литература

 Кафедра ЭМ

Применение полевых методов в электромагнитных расчетах электрических машин

1.3.3. Определение коэффициентов ξd, ξq, и kqd, по методике Р.Рихтера

( 1     2     3     4 )

Методика Р. Рихтера, по которой определяются поправочные коэффициенты, учитывающие насыщение стали при расчете главных индуктивных сопротивлений якоря по продольной и поперечной осям, достаточно подробно описана в [1-4, гл 55]. Суть ее заключается в том, чтобы, пользуясь результатами расчетов поля при заданных по отдельности и совместно МДС якоря и возбуждения F_dm, F_qm, F_fm и частичной характеристикой холостого хода E_f(F₁), где F₁ – магнитное напряжение зазора, зубцов и ярма статора, найти эквивалентные МДС обмотки возбуждения и, сравнив их с соответствующими эквивалентными МДС в ненасыщенной машине, определить поправки.

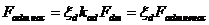                                             (1.21)

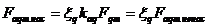                                             (1.22)

При этом оказалось удобным поперечную МДС якоря F_qm эквивалентировать не только магнитодвижущей силой F_aqm.нас, действующей по поперечной оси, но и появляющейся при насыщении магнитодвижущей силой F_qdm.нас , оказывающей влияние на продольное поле:

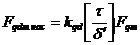,                                                         (1.23)

Для нахождения коэффициентов ξ_d , ξ_q и k_qd нужно решить три полевые задачи: при заданной МДС возбуждения F_fm, при совместном задании МДС возбуждения и продольной МДС обмотки якоря МДС F_dm и, наконец, при совместном задании всех трех МДС: F_fm, F_dm и F_qm. В каждом случае необходимо найти основные гармоники индукции поля в зазоре и рассчитать соответствующие им ЭДС (при задании всех трех МДС надо найти, кроме того,  составляющие основной гармоники индукции по продольной и поперечной осям).

Конечно-элементная модель, на которой могут быть рассчитаны все три поля, показана на рис. 1.20. Основные размеры модели взяты такими же, как и для генератора в примере расчета в [1-5], изменены только размеры зубцов – при сохранении ширины пазов число их увеличено (до q = 3) с тем, чтобы можно было ограничиться одним периодом поля (двумя полюсными делениями).

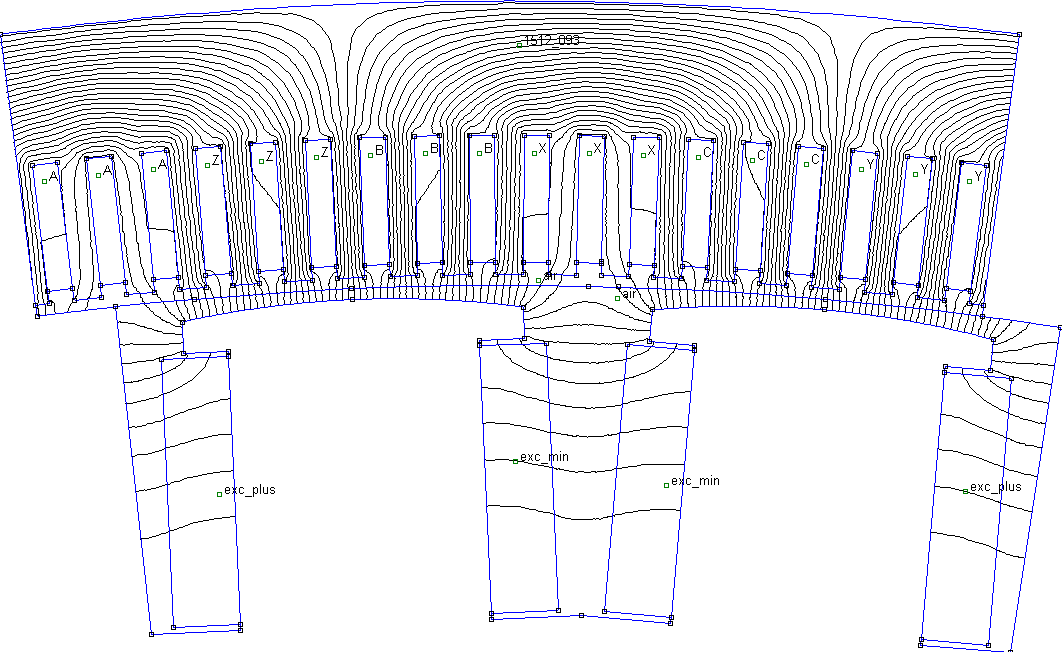
Рис. 1.20. Картина поля при холостом ходе. На боковых границах модели заданы периодические условия.

Для простоты обмотка якоря принята однослойной. Положение ротора относительно статора выбрано таким, чтобы в момент времени, когда ток в фазе А равен максимальному значению (ωt = 0), магнитная ось обмотки совпадала бы с осью d ротора. Это позволяет сравнительно просто воспроизвести на той же модели поле, созданное совместным действием двух МДС - F_fm и F_dm, добавив на участках пазов статора плотности тока, соответствующие ωt = 0.

      На рис. 1.21, показано распределение поля при холостом ходе и его гармонический состав. Там же показана основная гармоника поля, амплитуда которой равна 1,176 Т. Фазовый угол основной гармоники индукции в зазоре равен 30 эл. град. Это объясняется тем, что начало контура, на котором снималось распределение индукции (крайняя левая точка на дуге, проведенной посередине зазора), смещено относительно начала полюсного деления ротора на этот угол.

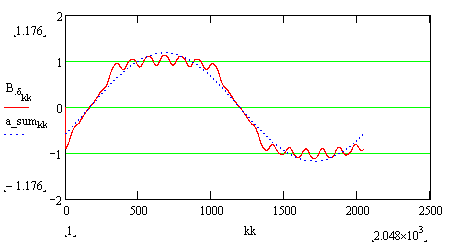
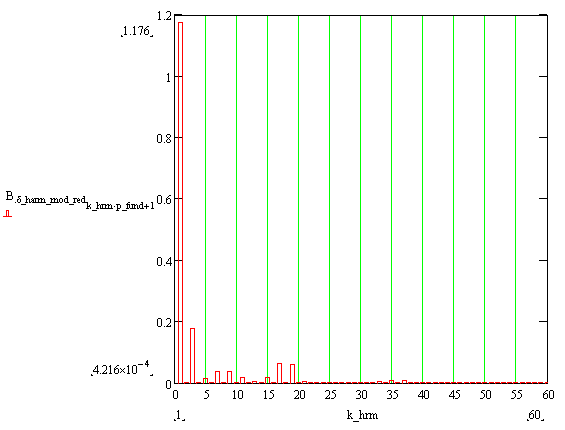
Рис. 1.21. Распределение индукции в зазоре и гармонический состав поля при холостом ходе. Максимальная индукция в зубцах равна 1,80 Т, в ярме – 1,37 Т.

Назад    Продолжение