Содержание

Часть 1

1.1

1.2

1.3

1.4

Часть 2

2.1

2.2

2.3

2.4

Часть 3

3.1

3.2

3.3

3.4

3.5

3.6

3.7

Литература

 Кафедра ЭМ

Применение полевых методов в электромагнитных расчетах электрических машин

2.4. Определение потерь в массивных сердечниках электрических машин

с помощью простых конечно-элементных моделей

  ( 1   2   3   4   5 )

В предыдущем параграфе уже говорилось о том, что при определенных допущениях простые конечно-элементные программы позволяют моделировать переменные электромагнитные поля в электропроводящих средах. Это, в свою очередь, позволяет рассматривать такие важные с практической точки зрения задачи, как определение потерь в массивных элементах обмоток и магнитопроводов. Имея в виду возможность моделировать МДС обмоток в виде гармонических токовых слоев, можно предложить достаточно простые конечно-элементные модели для определения потерь в массивных сердечниках, обусловленные как отдельными гармониками МДС, так и действующими совместно сопряженными пространственными гармониками.

При моделировании (и при обучении студентов работе с такими моделями) следует, однако, уделять особое внимание правильному формированию моделей и их конечно-элементной структуры. В связи с этим рассмотрим вначале на конкретном примере некоторые результаты моделирования поля при одном массивном сердечнике.

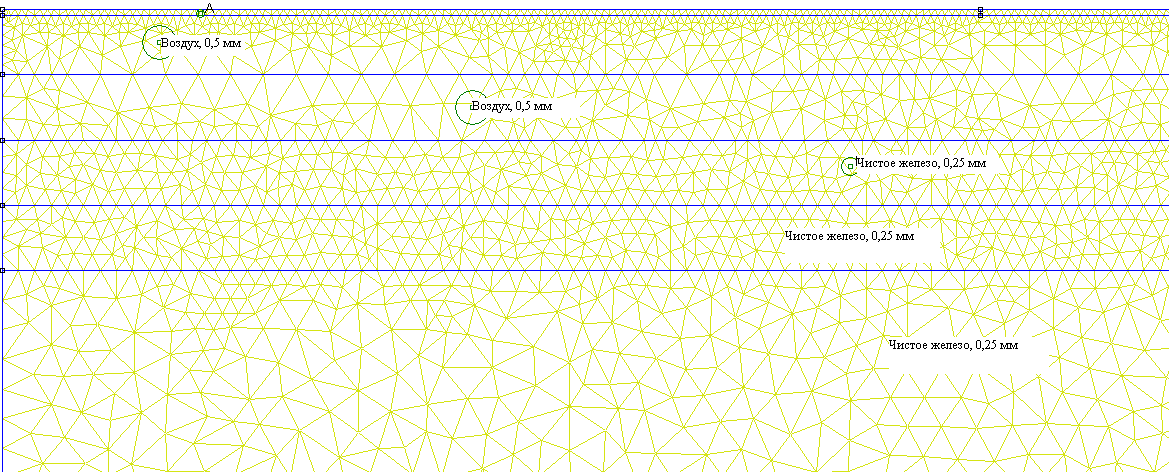
Рис. 2.34. Фрагмент конечно-элементной модели. Оба сердечника гладкие, возбужден верхний сердечник, нижний – массивный, с электрической проводимостью 10 МСм/м, с нелинейной кривой намагничивания

На рис. 2.34 показан фрагмент модели. Моделируется один период поля – двойное полюсное деление (360 мм). МДС возбужденного верхнего сердечника представлена тонким (0,1 мм) токовым слоем, состоящим из шести участков с постоянной плотностью тока на каждом из них (A, Z, B, X, C, Y). Амплитуда плотности тока равна 250 А/мм², разность аргументов комплексных значений плотности тока на соседних участках равна π/3. Зазор равен 2 мм. Нижний сердечник моделируется тремя слоями: двумя толщиной по одному мм и с размером конечных элементов 0,25 мм и слоем толщиной 5 мм с размером элементов 0,5 мм.

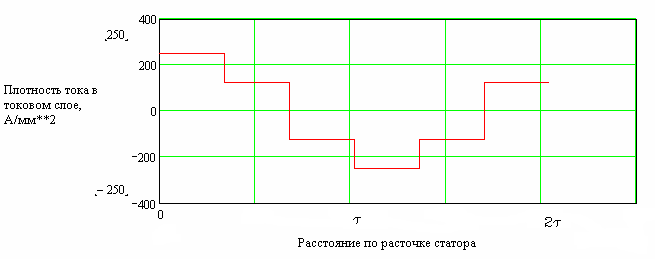
Рис. 2.35. Распределение плотности тока в токовом слое на поверхности возбужденного сердечника

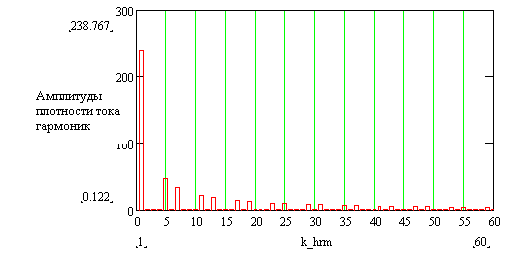
Рис. 2.36. Гармонический состав распределения плотности тока

в токовом слое

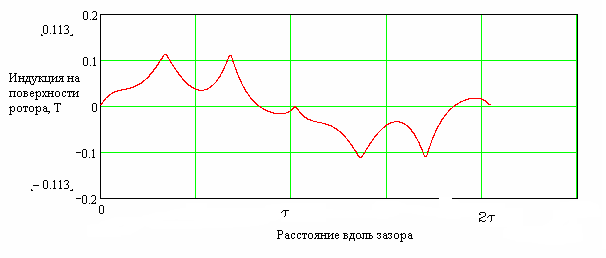
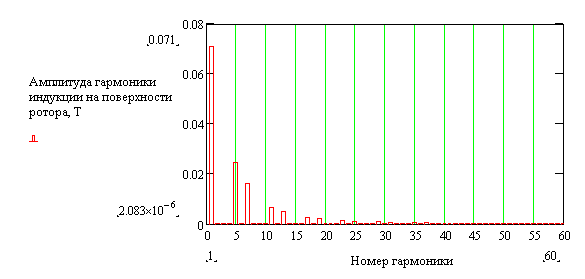
Распределение индукции на поверхности нижнего (массивного) сердечника и его гармонический состав показаны на рисунках 2.4.4. и 2.4.5.

Рис. 2.37. Распределение индукции на поверхности нижнего сердечника

Рис. 2.38. Гармонический состав распределения индукции на поверхности нижнего сердечника

  Назад   Продолжение