|
|
Применение полевых методов в электромагнитных расчетах электрических машин3.4.Определение результирующей ЭДС по результатам моделирования
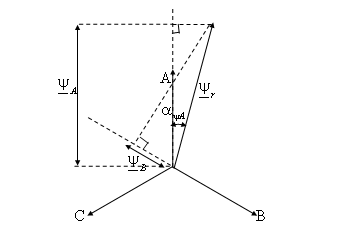
При моделировании режима нагрузки возможны два подхода, отличающиеся способом определения результирующей ЭДС обмотки якоря по результатам расчета поля. Первый из них прост – с помощью гармонического анализа распределения индукции в зазоре находятся амплитуда и пространственный фазовый угол основной гармоники индукции в зазоре. Как уже говорилось, при моделировании мгновенного состояния поля известно пространственное положение магнитной оси обмотки, таким образом, найденный фазовый угол основной гармоники определяет положение вектора индукции и, следовательно, вектора результирующей ЭДС на векторной диаграмме относительно вектора тока якоря. Далее при известных параметрах обмотки легко найти вектор напряжения и угол φ. Второй способ предполагает дифференцирование потокосцепления обмотки. Этот способ применялся, в частности, в диссертации А.И. Власова и М.А. Аванесовым при разработке программы TCPM, реализующей метод зубцовых контуров [3-7] применительно к расчету синхронных машин. Последовательное моделирование моментов времени с постоянным и достаточно малым интервалом между ними позволяет получить временную зависимость потокосцепления фазы обмотки с необходимой точностью. При использовании программы FEMM для проведения этой серии экспериментов лучше воспользоваться заранее составленной программой на языке Lua. Моделирование в этом случае усложняется и требует большего времени. Для учебных целей определение результирующего потокосцепления можно заметно упростить, не делая при этом большой ошибки. Если допустить, что результирующее потокосцепление может быть представлено вектором постоянной длины, вращающимся с постоянной скоростью, то мгновенные потокосцепления фаз могут рассматриваться как проекции этого вектора на направления магнитных осей фаз в рассматриваемый момент времени. При этом условии вектор результирующего потокосцепления может быть полностью определен по своим двум проекциям (рис. 3.11). Потокосцепления фаз в модельном эксперименте находятся как разности средневзвешенных значений векторных магнитных потенциалов на участках, соответствующих начальным и конечным сторонам катушек фаз.
Рис. 3.11. Определение результирующего потокосцепления трехфазной обмотки по двум измеренным на модели мгновенным значениям потокосцеплений фаз.
Расчетную длину машины при определении результирующей ЭДС обмотки якоря по результатам моделирования также можно выбрать различным образом. Влияние радиальных каналов на проводимость зазора и, следовательно, на расчетную длину можно учесть так, как это сделано, например, в [3-3], рассчитав должным образом коэффициент зазора. Как уже было замечено выше, влияние трехмерной неоднородности при моделировании по методу конечных элементов обсуждается в [3-6]. Поскольку уменьшение проводимости зазора за счет радиальных каналов, рифления ротора и увеличения зазора вблизи торцевых зон частично компенсируется выпучиванием поля на краях сердечников, приближенно расчетную длину можно взять равной полной длине сердечника статора. Итак, определив тем или иным способом вектор результирующей ЭДС и достроив векторную диаграмму, пользуясь заранее рассчитанными значениями параметров обмотки якоря, можно найти фазное напряжение и коэффициент мощности, т.е. найдя все данные режима работы. Если напряжение и/или коэффициент мощности не соответствуют номинальным значениям, следует скорректировать исходные данные модели – ток в обмотке возбуждения и/или угловое положение ротора относительно статора. Обычно для достижения требуемого соответствия достаточно трех-пяти итераций. В результате выполненных действий оказывается определенным ток обмотки возбуждения. Заметим, что при этом насыщение магнитной цепи учитывается наиболее полно. Непосредственно по результатам моделирования могут быть также определены индукции и падения магнитного напряжения в отдельных элементах магнитной цепи, электромагнитный момент и электромагнитная мощность, гармонический состав поля в зазоре.
|