Содержание

Часть 1

1.1

1.2

1.3

1.4

Часть 2

2.1

2.2

2.3

2.4

Часть 3

3.1

3.2

3.3

3.4

3.5

3.6

3.7

Литература

 Кафедра ЭМ

Применение полевых методов в электромагнитных расчетах электрических машин

3.6.Результаты моделирования

 ( 1   2  )

Примечания к  табл.3.2. Обозначения столбцов: 1 – расчет по традиционной методике; 2 - моделирование при расчетном токе возбуждения: 3 – моделирование при k_E = 1 при определении ЭДС по основной гармонике поля в зазоре;

Значение ЭДС генератора №2, приведенное в столбце 2, найдено по амплитуде основной гармоники индукции в зазоре B_δ1 при расчетной длине, равной полной длине сердечника (485 мм). При расчетной длине, использованной в примере расчета (445 мм), ЭДС получается на 2,8% меньше полученной в примере расчета. При полной длине, уменьшенной в 1,05 раз (составляющая коэффициента зазора, учитывающая наличие радиальных каналов) ЭДС получается на 4,2% больше приведенной в расчете. Значения ЭДС, найденные по потокосцеплениям фаз обмотки, для этого генератора практически равны ЭДС, рассчитанным по B_δ1.

Для генератора №3 при определении ЭДС в столбцах 2 и 3 расчетная длина принята равной полной длине сердечника статора (4200 мм), влияние вентиляционных каналов учтено тем, что использована эквивалентная относительная магнитная проницаемость для зазора (µ_r = 0,95). Значения потока в столбцах 2 и 3 найдены интегрированием нормальной составляющей индукции по средней линии зазора. ЭДС холостого хода, равная номинальному фазному напряжению, при определении ЭДС по потокосцеплениям фаз получается при F_f = 66380 А, что всего на 2,2% отличается от МДС возбуждения, полученной в примере расчета [3-4]. Картина поля в поперечном сечении генератора №3 при номинальной нагрузке показана на рис. 3.12.

Таблица 3.3

Расчет и моделирование номинальных режимов генераторов №№ 1,2,3.

Примечания к табл. 3.3.

1. В столбцах «расчет» приведены данные примеров расчета из соответственно [3-3, 3-4, 3-5]. В следующих двух столбцах приведены данные моделирования номинального режима при определении результирующей ЭДС по амплитуде основной гармоники индукции в зазоре (мод. А) и по мгновенным значениям потокосцеплений двух фаз (мод. В).

2. В качестве расчетной длины во всех случаях взята полная длина сердечника статора. Для турбогенератора (№3) влияние радиальных вентиляционных каналов на проводимость зазора учтено изменением относительной магнитной проницаемости зазора (µ_к = 0,95 < 1).

3. Δ(I_f) – расхождение между током возбуждения, полученным при моделировании, и его значением, приведенным в примере расчета.  

4. P_femm – электромагнитная мощность, рассчитанная по моменту, найденному по максвелловским натяжениям (интегрирование по средней линии воздушного зазора).

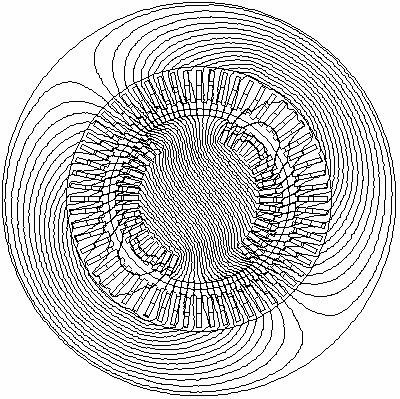
Рис. 3.12. Картина поля в поперечном сечении турбогенератора 200 МВт при номинальной  нагрузке  [3-5]

     Результаты, полученные на простых конечно-элементных моделях синхронных генераторов, оказываются весьма близкими к результатам расчетов по традиционным методикам. Применение таких моделей целесообразно ввести в практику учебного проектирования.

    При формировании конечно-элементных моделей крупных синхронных машин следует учитывать особенности, связанные с учетом трехмерной неоднородности магнитной системы и со способом определения результирующей ЭДС якоря.

  Назад   Продолжение