|
Исследование переходных процессов в ветви RLC
Введение
Исследуется зависимость i(t) при включении напряжения в ветвь с последовательным соединением сопротивления R, индуктивности L и емкости С. Переходной процесс в такой ветви описывается ДУ
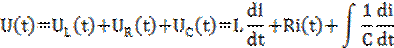
где
i(t) определяется как
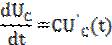
В форме
Коши уравнение (2.8) имеет вид системы
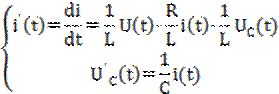(2.9)
Аналитическое решение (2.9) относительно тока i(t)
при включении постоянного напряжения U(t)=U
[2] для апериодического процесса имеет вид
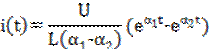(2.10)
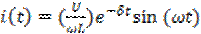- для колебательного процесса (2.11)
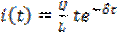- для критического (2.12)
где
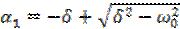и
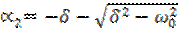- корни характеристического уравнения;
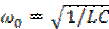– угловая резонансная частота;
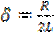– коэффициент затухания контура;
 –
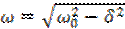угловая частота. Cоставление структурных блок-схем
Моделирование зависимости i(t) (2.10) на основании системы ДУ (2.9) для U(t) = U требует три решающих блока. Два блока интегросумматора необходимы для снижения порядка производных i'(t) и U'C(t), т.е. получения зависимостей i(t) и UC(t), и один блок константы - для задания коэффициента U/L на вход первого интегросумматора. При этом на входы 1, Р2 и РЗ первого блока интегросумматора должна подаваться сумма всех членов правой части первого уравнения (2.9), отождествляющая старшую производную исследуемого параметра, в частности i'(t), для получения с его выхода i(t). На вход второго интегратора должно быть подано отношение i(t)/C, равное U'C(t), для получения с его выхода UC(t). Структурная блок-схема для моделирования системы ДУ (2.9) показана на рис. 2.4.
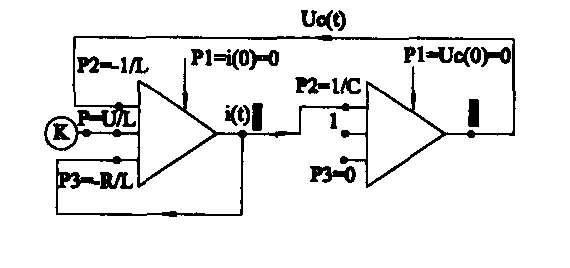
Рис 2.4
|
