|
Рассматривая далее ν как
алгебраическую величину, заменим в (49) и (44) ν его выражением
по (55). После несложных преобразований получим удобные для
анализа расчетные выражения для коэффициентов распределения
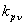 и укорочения и укорочения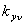 и обмоточного коэффициента и обмоточного коэффициента
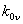 . Из приведенных формул отчетливо видно, что
коэффициенты распределения . Из приведенных формул отчетливо видно, что
коэффициенты распределения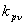 ,укорочения ,укорочения
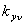 ,а поэтому и обмоточный коэффициент ,а поэтому и обмоточный коэффициент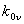 для гармонических, значение порядка которых
определяются при фиксированном значении j для гармонических, значение порядка которых
определяются при фиксированном значении j
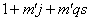 .
.
разных
значениях s, будут одинаковы в
общем случае с точностью до знака. Такие гармонические принято
называть сопутствующими. Главное значение имеют гармонические,
сопутствующие основной и определяемые при
j = 0 и
s = ±l.
Число
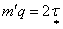 , совпадающее с
числом зубцовых делений на двойном полюсном делении,
представляет собой период обмоточных коэффициентов. , совпадающее с
числом зубцовых делений на двойном полюсном делении,
представляет собой период обмоточных коэффициентов.
Из
сказанного выше следует, что устранить гармонические МДС,
сопутствующие основной гармонической (называемые часто
гармоническими зубцового порядка, поскольку их порядок равен
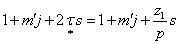
и при
j
=
0 и
s
= 0 мало отличается от числа зубцов
z1),
невозможно воздействием на коэффициенты распределения и
укорочения. С этой целью прибегают к применению скоса пазов
(рис. 2.5,а). При необходимости учета этого скоса, например при
воздействии МДС и магнитного поля «скошенной» обмотки на
нескошенную обмотку другого сердечника, этого можно добиться
путем внесения соответствующих изменений в математическую модель
МДС зубцового контура, которая в этом случае (рис. 2.5,6) имеет
трапецеидальную форму: трапеция с основаниями
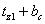 и и
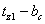 и высотой и высотой
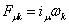 . .
|





 |