|
Цель работы -
моделирование на ПЭВМ дифференциальных уравнений (ДУ) асинхронного двигателя (АД)
с короткозамкнутым ротором и исследование основных динамических и статических
характеристик.
Введение
Уравнения
электрического равновесия, описывающие электромагнитные переходные процессы в
АД с короткозамкнутым ротором, известны в различных формах записи. Выбор системы
координат, вращающейся со скоростью ωk,
зависит от рассматриваемой задачи: при несимметрии статора удобны координаты
α,β статора, т.е. ωk = 0; при
несимметрии ротора - координаты
d,q ротора, т.е. ωk
= ωг, где ωг = ω1(1- s)
- электрическая угловая скорость ротора, ω1=2πf1
- электрическая угловая скорость поля статора и
f1 - частота сети. При
симметричном питании целесообразно применять координаты
u,v синхронных осей, т.е. ωk
= ω1 так как в этих осях неподвижны векторы напряжений и токи в
установившемся режиме, следовательно, быстрее достигается сходимость решения.
При общепринятых в теории
электрических машин допущениях ДУ асинхронного двигателя в системе координат
u,v, вращающихся с произвольной
скоростью ωk
имеют вид [3 и 4]
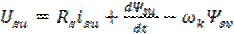 ; ;
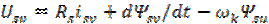 ; ;
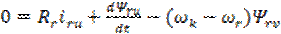 ;
(3.1) ;
(3.1)
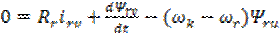 , ,
где напряжения питания
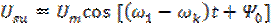 и и
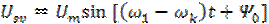 .
(3.2) .
(3.2)
Потокосцепления обмоток статора и ротора
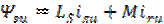 и и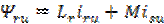 ; ;
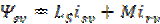 и и
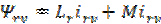 , ,
где
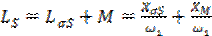 , ,
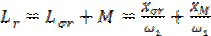 ;
RS и
XσS –
активное и индуктивное сопротивления рассеяния обмотки статора;
Rr
и Хσr
– активное и индуктивное сопротивления рассеяния обмотки ротора,
приведенные к числу витков и фаз обмотки статора;
М - взаимная индуктивность; ;
RS и
XσS –
активное и индуктивное сопротивления рассеяния обмотки статора;
Rr
и Хσr
– активное и индуктивное сопротивления рассеяния обмотки ротора,
приведенные к числу витков и фаз обмотки статора;
М - взаимная индуктивность;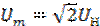 ,
биноминальное фазовое напряжение; Ψ0 - начальная фаза
включения напряжения; isu, isv
, iru
и irv
– токи в обмотке статора и приведённые токи в обмотке ротора. ,
биноминальное фазовое напряжение; Ψ0 - начальная фаза
включения напряжения; isu, isv
, iru
и irv
– токи в обмотке статора и приведённые токи в обмотке ротора.
Если ротор вращается с
переменной угловой скоростью, то его движение описывается уравнением
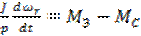 ,
(3.4) ,
(3.4)
где
J – момент инерции ротора и приведенного момента
инерции нагрузочного механизма;
р -
число пар полюсов;
МС
- момент сопротивления;
МЭ
- электромагнитный момент АД равный
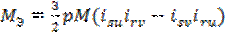 .
(3.5) .
(3.5)
|
