|
Для построения модели наиболее удобны уравнения, в которых искомыми переменными
являются потокосцепления. В этом случае модель требует минимального числа
решающих блоков и получается устойчивой. Чтобы исключить токи, выразим их через
потокосцепления, используя соотношения
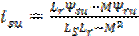 и и
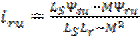 ; ;
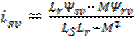 и и
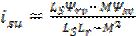 (3.6)
(3.6)
Система ДУ, преобразованная к
виду, удобному для моделирования АД в координатах осей α,β (ωk=0)
на основании (3.1- 3.6), имеет вид
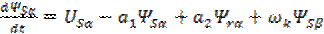 ; ;
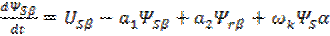 ; ;
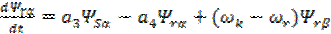 ;
(3.7) ;
(3.7)
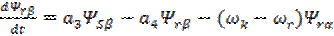 ; ;
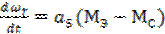 ; ;
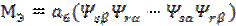 , ,
где
коэффициенты при переменных равны: 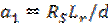 ; ;
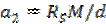 ; ;
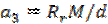 ; ;
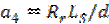 ; ;
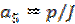 ; ;
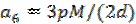 ; ;
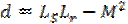 . .
В
преобразованной системе токи в явном виде отсутствуют, однако при необходимости
они могут быть определены из (3.6). Токи статора и ротора в осях α,β на
основании (3.6) можно записать с помощью коэффициентов при переменных как
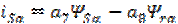 ; ;
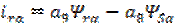 ,
(3.8) ,
(3.8)
где
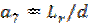 ; ;
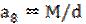 ; ;
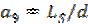 . .
Гармонические функции в (3.7),
определяющие напряжения питания, равны
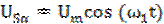 и и
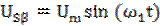 . .
|
