|
Исследование переходного процесса в ветви RL
Введение
Исследуется зависимость тока от времени i(t) с момента включения напряжения и с момента закорачивания его в цепи с последовательным соединением активного сопротивления R = const и индуктивности L = const. Переходный процесс в такой ветви описывается ДУ
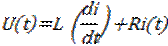
(2.4)
В форме Коши ДУ (2.4) имеет вид
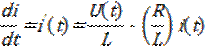 (2.5)
(2.5)
Аналитическое решение (2.5) относительно тока i(t) с момента подключе¬ния постоянного напряжения U(t) = U к ветви
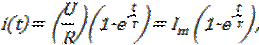 (2.6) (2.6)
где зависимость i(t) имеет вид возрастающей экспоненты, а с момента закорачивания
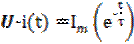 - убывающей экспоненты [2]. (2.7)
- убывающей экспоненты [2]. (2.7)
Составление структурных блок-схем
Для получения зависимости i(t) (2.6) или (2.7) требуется смоделировать ДУ (2.5), где для определения i(t) по (2.6) U = const, а для определения i(t) по (2.7) U = 0 для t > 0 и U= const для t = 0.
Для моделирования ДУ или системы ДУ в форме Коши необходимо составить блок-схему, вид которой может иметь несколько вариантов, один из которых оптимальный. Например, для (2.5) блок-схема имеет два варианта. Первый - составление блок-схемы непосредственно по уравнению. Правая часть (2.5) содер жит два члена - значит требуется решающий блок сумматора, при этом один из членов является константой - нужен решающий блок константы, а для получения i(t) необходим решающий блок интегратора.
На рис. 2.3а и 2.3б показаны структурные блок-схемы для определения I(T) соответственно (2.6) и (2.7). Блок константы (см. рис. 2.3б) отсутствует, так как его коэффициент Р = U/L = 0.
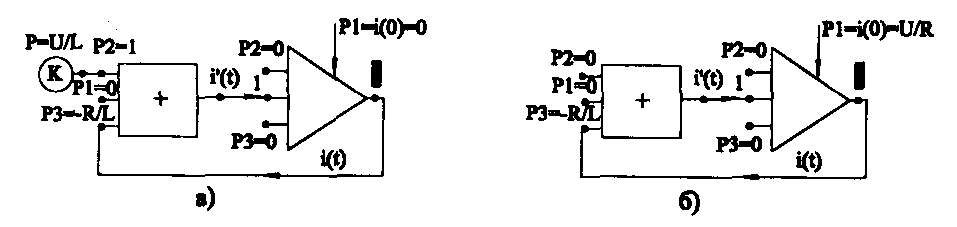
Рис.2.3
При составлении блок-схемы для (2.5) по второму (оптимальному) варианту можно вместо блоков сумматора и интегратора использовать только блок интегросумматор, так как этот блок выполняет дополнительно суммирование функций, т.е. является интегросумматором. Оптимальный вариант содержит меньшее количество решающих блоков в структурной схеме, что упрощает ее набор, снижает время счета и повышает точность расчета. Оптимальный вариант может потребовать большее количество расчетных коэффициентов.
Составление оптимальных блок-схем на основании ДУ (2.5) для определения зависимости i(t) согласно (2.6) и (2.7) выполняется студентами самостоятельно. В последующих лабораторных работах все блок-схемы приведены для оптимальных вариантов.
|
