|
Последнее обстоятельство указывает
пути построения математической модели МДС, основанные на замене
неизвестного распределения плотности тока некоторым расчетным
близким к нему распределением. При этом возможны два подхода:
а) действительное неизвестное
распределение тока в слое заменяется расчетным с постоянной
плотностью, определяемой из уравнения:
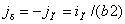 (6)
(6)
б) вместо поверхностного слоя тока вводится сосредоточенный
линейный ток, совпадающий по величине и знаку с током паза и
размещаемый со стороны зазора в точке пересечения оси паза с
прямой 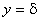 . .
На
рис. 2.2 для трех различных
математических моделей поверхностных слоев тока представлены
зависимости распределения скалярного магнитного потенциала на
поверхности 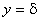 при условии, что возбужден только один «k»-й
зубцовый контур, а токи во всех прочих контурах обоих
сердечников равны нулю. при условии, что возбужден только один «k»-й
зубцовый контур, а токи во всех прочих контурах обоих
сердечников равны нулю.
Математической
моделью МДС, изображенной на рис.
2.2,а, практически воспользоваться не удается,
поскольку точное распределение линейной плотности в
поверхностных токовых слоях заранее неизвестно. На
рис. 2.2,6 и
2.2,в вместо действительной зависимости
скалярного магнитного потенциала на поверхности
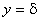 представлены идеализированные зависимости представлены идеализированные зависимости
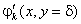 и и
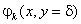 в виде соответственно трапецеидального и
прямоугольного импульсов. в виде соответственно трапецеидального и
прямоугольного импульсов.
|