|
Полная
проводимость пазового рассеяния, включающая в себя проводимость
для потокосцепления пазового рассеяния в области паза, занятого
проводником с током 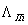 (рис. 2.12в) (рис. 2.12в)
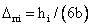 (123)
(123)
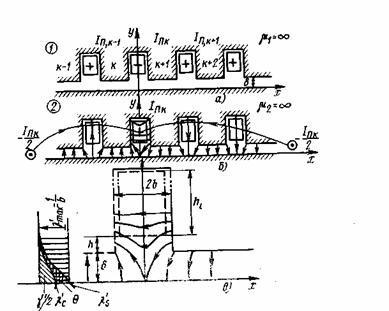
рис.2.12
и магнитную
проводимость для потоков и потокосцеплений рассеяния в шлицевой
части паза
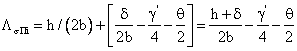 (124) (124)
|
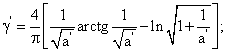
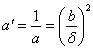 ; ; |
(125) |
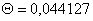 (126)
(126)
В практических расчетах применяют
формулу, получающуюся из (120) введением в нее вместо числа
витков паза 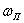 числа витков фазы числа витков фазы
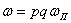 : :
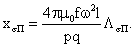 (127)
(127)
При укорочении шага обмотки (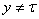 ) в части пазов находятся катушечные стороны
разных фаз. Так как токи прямой последовательности сдвинуты во
времени, то потокосцепления от полей рассеяния с учетом влияния
фаз друг на друга будут слабее в этих пазах. Влияние укорочения
шага на индуктивное сопротивление пазового рассеяния учитывается
коэффициентом ) в части пазов находятся катушечные стороны
разных фаз. Так как токи прямой последовательности сдвинуты во
времени, то потокосцепления от полей рассеяния с учетом влияния
фаз друг на друга будут слабее в этих пазах. Влияние укорочения
шага на индуктивное сопротивление пазового рассеяния учитывается
коэффициентом 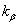
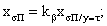 (128)
(128)
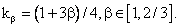 (129) (129)
Для токов
обратной последовательности индуктивное сопротивление пазового
рассеяния рассчитывается аналогично.
Индуктивное сопротивление для токов
нулевой последовательности при
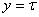 получается таким же, как и для системы токов
прямой и обратной последовательностей, так как при отсутствии
укорочения шага в пазу находятся проводники одной фазы. При получается таким же, как и для системы токов
прямой и обратной последовательностей, так как при отсутствии
укорочения шага в пазу находятся проводники одной фазы. При
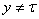 вновь появляется взаимное влияние фаз, но при
этом же необходимо учитывать совпадение токов фаз во времени.
Коэффициент вновь появляется взаимное влияние фаз, но при
этом же необходимо учитывать совпадение токов фаз во времени.
Коэффициент 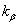 в этом случае рассчитывается по формуле в этом случае рассчитывается по формуле
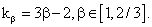 (130)
(130)
|