|
Особенность такой диаграммы
заключается в том, что с действительной осью .комплексной
плоскости совмещается не только ось отсчета времени и связанных
с временной переменной t
электрических углов wt,
но и пространственная ось главной фазы (фазы «А»). Другими
словами, действительная ось комплексной плоскости является
одновременно и осью отсчета пространственных электрических углов
по «n»-ой
гармонической. При этом положительные направления осей трех фаз
«А», «Б» и «С» будут изображаться на этой диаграмме следующими
ортами-комплексами (положение этих векторов на диаграмме
неизменно и от времени не зависит):
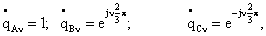 91) 91)
Векторы тока
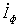 (действующее значение) и потокосцепления (действующее значение) и потокосцепления
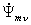 (амплитудное значение), напротив,
перемещаются с угловой электрической скоростью
w, и их положение на
комплексной плоскости в рассматриваемый момент времени
t определяется углом
wt,
как показано на рис. 2.8. (амплитудное значение), напротив,
перемещаются с угловой электрической скоростью
w, и их положение на
комплексной плоскости в рассматриваемый момент времени
t определяется углом
wt,
как показано на рис. 2.8.
Мгновенное значение потокосцепления
с фазой «A»
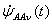 в момент времени t
условимся рассматривать как некоторый комплекс в момент времени t
условимся рассматривать как некоторый комплекс
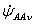 , который представляет собой полусумму
комплексных функций , который представляет собой полусумму
комплексных функций 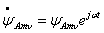 и и
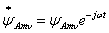 : :
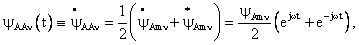 (92) (92)
Потокосцепление взаимоиндукции фазы А в тот же момент времени с
произвольной «m»-й фазы
можно определить как скалярное произведение комплексов
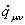 и и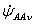 : :
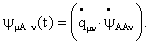 (93)
(93)
С тем, чтобы отличить обычное
произведение двух комплексов
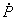 и и
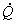 от их скалярного произведения, условимся в
последнем случае заключать эти комплексы в круглые скобки и,
кроме того, между самими комплексами ставить признак умножения —
точку. Непосредственным вычислением нетрудно убедиться в
справедливости следующего соотношения: от их скалярного произведения, условимся в
последнем случае заключать эти комплексы в круглые скобки и,
кроме того, между самими комплексами ставить признак умножения —
точку. Непосредственным вычислением нетрудно убедиться в
справедливости следующего соотношения:
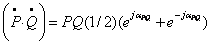 , (94) , (94)
где
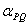 — пространственный (электрический) угол между
комплексами — пространственный (электрический) угол между
комплексами 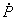 и и
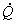 . .
В соответствии с приведенным
алгоритмом определим, к примеру, индуктивность взаимоиндукции
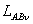 . Получим в итоге . Получим в итоге
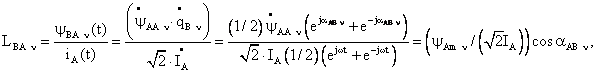 (95) (95)
где
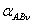 — электрический угол между осями фаз «A»
и «В» в пространстве для «n»-й
гармонической поля. Описанный подход к определению
индуктивностей — электрический угол между осями фаз «A»
и «В» в пространстве для «n»-й
гармонической поля. Описанный подход к определению
индуктивностей 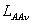 и и
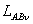 применим при любом числе фаз
m. При этом электрический угол
между осями соседних фаз для основной гармонической поля
определяется из уравнений применим при любом числе фаз
m. При этом электрический угол
между осями соседних фаз для основной гармонической поля
определяется из уравнений
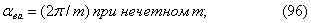
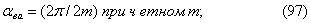
|