|
П.1. Некоторые
соотношения между тригонометрическими и гиперболическими
функциями комплексного аргумента и их выражения через
тригонометрические и гиперболические функции действительного
аргумента
Указанные соотношения могут быть
легко получены, исходя из формулы Эйлера, которая связывает
между собой показательную функцию с показателем степени, равным
комплексному аргументу
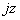 ,
и тригонометрические функции с комплексным аргументом ,
и тригонометрические функции с комплексным аргументом
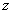 : :
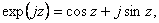 (63) (63)
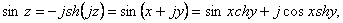 (64) (64)
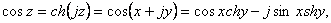 (65) (65)
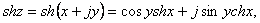 (66) (66)
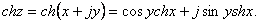 (67) (67)
Обратные тригонометрические и
гиперболические функции комплексного аргумента
 определяются
так же, как и для действительного аргумента. Например, определяются
так же, как и для действительного аргумента. Например,
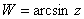 ,
если ,
если 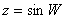 .
По определению .
По определению
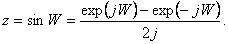 (68) (68)
Обозначим
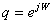 и
заменим переменную и
заменим переменную 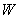 в
(68) на в
(68) на 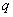 .
Уравнение (68) преобразуется к виду .
Уравнение (68) преобразуется к виду
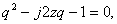 (69) (69)
откуда
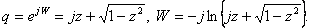 (70) (70)
Аналогично могут быть получены и
прочие обратные тригонометрические и гиперболические функции
 (71) (71) |