Лабораторная работа № 1
Расчет магнитного поля в зазоре
электрической машины методом конечных разностей для различных способов
намагничивания
Методические указания. Метод расчета
Расчет магнитного поля в данной работе проводится методом конечных
разностей. Основная его идея состоит в замене производных их
приближенными конечноразностными выражениями, разностями значений
функции поля в узлах.
В области безвихревого поля справедливо уравнение Лапласа, где неизвестной
функцией является скалярный магнитный потенциал U:
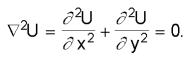
Покроем область магнитного поля расчетной квадратной сеткой (рис. 3). Для упрощения выберем bz, bп и δ кратными размеру ячейки сетки. Необходимо найти значение функции U в узлах квадратной сетки.
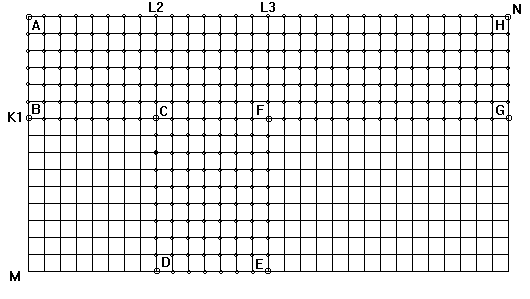
Рис. 3.
Для любого произвольного внутреннего (не лежащего на границе) узла области U(m,n) (рис. 4) конечноразностная аппроксимация уравнения Лапласа может
быть выражена так:
U(m-1,n)+U(m,n-1)+U(m+1,n)+U(m,n+1)-4U(m,n)=0.
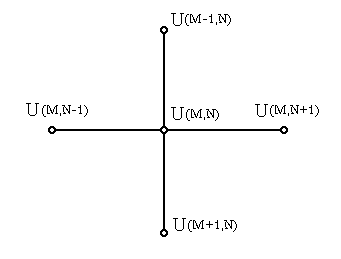
Аналогично могут быть записаны уравнения и для всех остальных внутренних
точек области поля. В часть этих уравнений
Одним из наиболее простых методов решения является итерационный. На первом
этапе расчета произвольно задаются распределением искомой функции во
всей области решения, например, полагают значения искомой функции во
всех внутренних точках области равными нулю. Значения функции в
граничных точках задают в соответствии с граничными условиями. Для
каждого узла сетки рассчитывают значение так называемого остатка RES(m,n),
равного
RES(m,n)=U(m-1,n)+U(m+1,n)+U(m,n-1)+U(m,n+1)-4U(m,n).
Уравнение Лапласа будет удовлетворяться, если все остатки станут равными
нулю. Для сокращения затрат машинного времени обычно задаются определенным
максимально допустимым уровнем остатка, при достижении которого счет
прекращается.
В данной работе определяется влияние задаваемой погрешности EPS (т.е.
максимально допустимого остатка) на количество итераций.
Итак, если для n-ой итерации наибольшее RES(m,n) оказалось больше заранее
обусловленного значения EPS, то значение функции в точке (m,n)
корректируется и для (n+1) итерации принимается равным
Un+1(m,n)=Un(m,n)+w×RES(m,n)/4,
где коэффициент
w
(в программе - OMEGA) носит название коэффициента релаксации и обычно
выбирается в пределах от 1 до 2. Данная формула реализует экстраполяционный
метод Либмана.
При коэффициентах релаксации, близких к 1, решение сходится медленнее, а
при близких или больших 2 - может стать неустойчивым. Подбор оптимального
коэффициента релаксации входит в программу данной работы.
Результатом решения являются значения функции поля в узлах сетки,
наложенной на область поля. Значение индукции B (градиента найденной функции
U) определяется следующим образом:
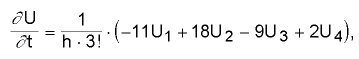
где U1, U2, U3, U4
- значения функции поля в узлах, отстоящих друг от друга на расстоянии шага
h и лежащих на прямой, параллельной направлению
t.