Решение задач электромеханики на

Лабораторная работа № 3
Исследование переходных процессов в асинхронном двигателе c короткозамкнутым ротором при моделировании в осях a,b

Методические указания к пункту 1

Для исследования асинхронных двигателей с симметричными обмотками удобна система ортогональных координат a,b, неподвижных относительно статора [1]. Уравнения равновесия напряжений обобщенной машины записываются при этом в следующем виде:

В уравнения входят полные потокосцепления обмоток статора и ротора, которые складываются из потокосцеплений самоиндукции и взаимоиндукции:

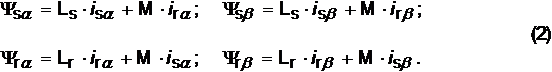
Система уравнений (1) может быть решена относительно потокосцеплений, если входящие в нее токи выразить через потокосцепления по формулам:

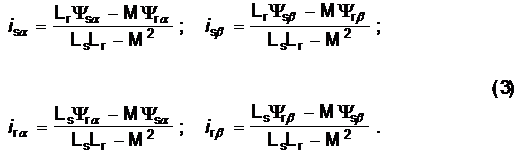
Система уравнений, в которой искомыми переменными являются потокосцепления, наиболее устойчива и удобна для интегрирования. Токи при необходимости можно для любого режима определить из алгебраических уравнений (3).

Так как для машины с короткозамкнутым ротором

U_s_a=U_m×COSωt; U_s_b=U_m×SINωt; U_r_a=U_r_b=0.

то уравнения имеют вид:

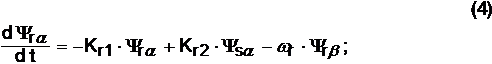
Здесь

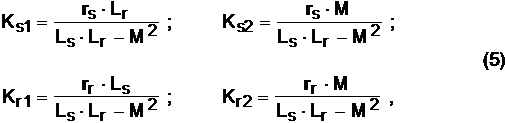
ω=2πf - угловая частота напряжения сети.

На ротор асинхронного двигателя в общем случае действует сумма моментов, определяющая закон изменения его скорости вращения во времени. В эту сумму входят:

1) Динамический момент, равный

Здесь J - сумма момента инерции ротора двигателя и приведенного момента инерции нагрузочного механизма; p - число пар полюсов двигателя.

Отметим, что частота вращения ротора в геометрических радианах в секунду ω₂ связана с ω_r соотношением ω₂=ω_r/p. По ω₂ можно найти частоту вращения n (об/мин), если воспользоваться формулой

2) Демпфирующий момент, равный

где B - коэффициент демпфирования. Этот момент в асинхронном двигателе физически обычно эквивалентен моменту трения (моменту механических потерь). Момент трения в подшипниках может составлять значительную долю от номинального момента в машинах малой мощности. При моделировании асинхронных двигателей средней и большой мощности приближенно можно считать, что момент трения равен 1% от номинального момента M_н при номинальной частоте вращения ω_r_н:

Большинство асинхронных двигателей имеет вентилятор на валу. Так как вентиляторный момент (как и момент трения ротора о воздух) является квадратичной функцией частоты вращения и не велик по сравнению с другими слагаемыми в уравнении момента, будем считать при моделировании, что оба момента учитываются в результирующем моменте трения (6).

3) Момент нагрузки M_c. В общем случае M_c может быть произвольной функцией времени, которая должна быть задана. В данной работе предусмотрен лишь постоянный момент M_c.

4) Электромагнитный момент двигателя M_э. Как было отмечено выше, момент трения (механических потерь) входит в уравнение моментов в виде отдельного слагаемого. Поэтому вращающий момент асинхронного двигателя можно считать равным электромагнитному. Последний определяется через мгновенные значения потокосцеплений, найденных в результате решения уравнений (4). Уравнение электромагнитного момента для асинхронного двигателя (Н×м) имеет вид:

(7)

Запишем уравнение моментов асинхронного двигателя:

(8)

или

(9)

Уравнения (4) совместно с уравнением (9) образуют полную систему дифференциальных уравнений асинхронного двигателя с короткозамкнутым ротором.

Активные сопротивления r_s и r_r в дифференциальных уравнениях не отличаются от сопротивлений фаз статора и ротора, входящих в схему замещения для установившегося режима, т.е. при рабочей температуре берется r_s=r₁, r_r=r₂

Уравнения, представленные выше, одинаково справедливы как для действительных, так и для приведенных переменных и параметров ротора. Если ротор приводится к статору, то в уравнениях должны стоять только приведенные величины ротора.

Взаимная индуктивность M связана с индуктивным сопротивлением взаимоиндукции X₁₂ в схеме замещения:

M=X₁₂/ω. (10)

Полные индуктивности фаз обмоток статора и ротора определяются суммой потокосцеплений с рабочим потоком и потоком рассеяния. Поэтому:

L_s=(X₁₂+X₁)/ω; L_r=(X₁₂+X₂^’)/ω. (11)

Здесь X₁, X₂^’ - индуктивные сопротивления рассеяния из схемы замещения асинхронного двигателя.

В данной лабораторной работе исследуется модель серийного трехфазного асинхронного двигателя с короткозамкнутым ротором типа А42-6 со следующими номинальными данными: 1,7 кВт; 220/380 В; 7,5/4,3 А; 930 об/мин. Машина имеет кратность пускового тока 4,5; кратность пускового момента 1,4; кратность максимального момента 1,8.

Параметры двигателя при рабочей температуре 75°C равны:

r_sα=r_s_β=3,57 Ом - активное сопротивление обмотки статора по осям α и β;
r_rα=r_r_β=3,8 Ом - приведенное активное сопротивление обмотки ротора по осям α и β;
L_sα=L_s_β=0,2787 Гн - полные индуктивности обмотки статора по осям α и β;
L_rα=L_r_β=0,2892 Гн - полные индуктивности обмотки ротора по осям α и β;
M=0,2628 Гн - взаимная индуктивность;
J=1,491 Н×м×с² - кинетический момент инерции;
p=3 - число пар полюсов;
m=3 - число фаз;
M_н=11,87 Н×м - номинальный момент.

Обратимся теперь к способам решения системы дифференциальных уравнений.

Полная система уравнений (4) и (9) может быть записана в общем виде как

(12)

Для успешного решения системы обыкновенных дифференциальных уравнений первого порядка (12) необходимо задать начальные условия X(t₀)=X₀. При этом предполагается, что решение задачи для этих начальных условий существует и хорошо определено для всех моментов времени t>t₀. В нашем случае необходимо задание в момент времени t₀ величин потокосцеплений обмоток Y_sα(t₀), Y_sβ(t₀), Y_rα(t₀) и Y_rβ(t₀), а также угловой скорости вращения ротора ω_r(t₀).

Для нахождения X(t) численным методом весь интервал времени решения T делят на небольшие приращения времени. Каждое приращение времени h_i=(Δt)_i называют величиной шага. Целью численного интегрирования является нахождение функции X(t) в каждой точке разбиения интервала времени T. Большинство методов решения подобной задачи, называемой задачей Коши, базируется на двух основных подходах: разложение в ряд Тейлора и полиномиальная аппроксимация. Методы, основанные на разложении в ряд Тейлора, обычно называют методами Рунге-Кутта. Методы, основанные на полиномиальной аппроксимации, обычно называют методами численного интегрирования [2].

Для достижения достаточно высокой точности при относительно большой величине шага наиболее широко используется метод Рунге-Кутта четвертого порядка. Он задается следующими выражениями:

X_n+1=X_n+h×K₄(X_n,t_n,h), (13)

где K₄(X_n,t_n,h)=1/6×[k₁+2k₂+2k₃+k₄];

k₁=f(X_n,t_n);

k₂=f(X_n+h/2×k₁,t_n+h/2); (14)

k₃=f(X_n+h/2×k₂,t_n+h/2);

k₄=f(X_n+h×k₃,t_n+h).

Этот метод реализован в известной подпрограмме RKGS. Эта подпрограмма самостоятельно осуществляет интегрирование на заданном интервале. Пользователь должен лишь обеспечить расчет правой части системы дифференциальных уравнений. При этом существенно усложняется процесс управления ходом расчета и оперативного вмешательства в него.

Решение задач электромеханики на ЭВМ