|
Размагничивающее влияние поперечной МДС
Fq
на продольное поле эквивалентируется продольной МДС возбуждения
Fqd=ξqd
Faq
где
ξqd
— коэффициент, зависящий от Еr
(по рис. 2).
Направления комплексов МДС на векторной
диаграмме должны быть следующими:
МДС
F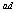 совпадает
по направлению с током совпадает
по направлению с током
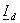 ; ;
МДС
F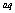 совпадает
по направлению с током совпадает
по направлению с током
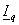 ; ;
МДС
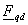 всегда
отстает от ЭДС Erd на угол
π/2. всегда
отстает от ЭДС Erd на угол
π/2.
Насыщенные значения индуктивных
сопротивлений взаимоиндукции также выражаются через коэффициенты
ξd
и ξq,:
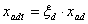 , ,
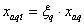 . .
При известных токах
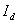 и и
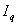 с
помощью этих параметров могут быть найдены ЭДС с
помощью этих параметров могут быть найдены ЭДС
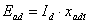 и и
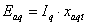 , ,
соответствующие этим токам, и затем по
спрямленной в начале координат характеристике холостого хода графически
определены (см. рис. 1) эквивалентные МДС
Fad
и Faq.
В этом случае отпадает необходимости в расчете МДС
Fd,
Fq,
и коэффициентов kad,
kaq.
Результирующая МДС по продольной оси
Frd,
соответствующая ЭДС
Erd
и опережающая последнюю на угол
π/2,
представляет собой сумму всех МДС, которые действуют по продольной оси
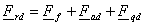 . .
Откуда МДС возбуждения при нагрузке,
определяемой из векторной диаграммы, равна
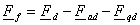 . .
Порядок построения диаграммы.
1. В произвольном масштабе откладывается
вектор тока I
в относительных единицах (единице тока может, например, соответствовать
отрезок длиной 50 или 100 мм).
2. Под углом
φ к вектору тока
I
строится вектор напряжения
U
в относительных единицах. Масштабы для напряжений и МДС удобно выбрать
такими же, как на нормальной характеристике холостого хода (единице
напряжения может, например, соответствовать отрезок длиной 100мм,
единице МДС — отрезок 50 мм).
3. Далее откладывается вектор
jxσI,
длина которого в выбранном масштабе соответствует напряжению
xσI
в относительных единицах. Определяется результирующая ЭДС в
относительных единицах
Er.
4. Для определения направления вектора
ЭДС Е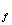 (или
угла ψ)
к вектору jxσI
прибавляется вектор
jxaqнI. (или
угла ψ)
к вектору jxσI
прибавляется вектор
jxaqнI.
5. Определяются продольная
Id
и поперечная Iq
составляющие тока.
6. По продолжению прямолинейного участка
характеристики холостого хода определяется магнитодвижущая сила обмотки
возбуждения Fad,
эквивалентная продольной МДС обмотки якоря. МДС
Fad
в относительных единицах соответствует напряжению
xadнId
в относительных единицах, где
xadн=xadξd
по рис.2. На диаграмме МДС
Fad
совпадает по направлению с током
Id.
7. Результирующая МДС
Frd
соответствует по характеристике холостого хода ЭДС
Erd
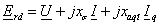 , ,
где
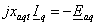 , ,
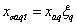 по
рис.2. по
рис.2.
На диаграмме комплекс МДС Frd
опережает на π/2
ЭДС Erd.
8. По продолжению прямолинейного участка
характеристики холостого хода определяется МДС
Faq,
эквивалентная поперечной МДС
якоря.
МДС
Faq
в относительных единицах
соответствует напряжению
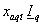 в
относительных единицах. в
относительных единицах.
9. Рассчитывается МДС
Fqd=ξqdFaq
эквивалентная
размагничивающему влиянию поперечной МДС на продольное поле (ξqd
по рис.2). На диаграмме эта
МДС откладывается в виде комплекса, отстающего на
π/2
от ЭДС Еrd.
10. МДС обмотки возбуждения в
относительных единицах
Ff=Frd-Fad-Fqd.
11. Ток возбуждения в абсолютных
единицах (амперах)
If=IfxFx.
Примечание. При построении диаграммы без
учета насыщения следует пользоваться характеристикой холостого хода,
полученной путем продолжения прямолинейного участка нормальной
характеристики.
Коэффициенты насыщения принимают в этом
случае следующие значения:
ξq=
ξd
=1;
ξqd=0.
Для
построения диаграммы без учета насыщения можно также обратиться к [1, с.
548].
1
2
3
4
5 |