1.5. Влияние поперечного магнитного поля на устойчивость
течения проводящей жидкости

Главная проблема исследования устойчивости потока жидкости заключается в установлении критериев, при которых ламинарное течение переходит в турбулентное. Теоретический анализ этой проблемы базируется на методе малых возмущений. Суть метода заключается в решении основных уравнений с переменными v+v', р+р', В+b' и т.д., где члены v', p', b' – добавленные величины возмущений. Эти возмущения очень малы по сравнению с соответствующими величинами, характеризующими основное течение. Решение задачи достаточно сложно. Как уже было замечено выше, целесообразно ограничиться только физическими представлениями и обсуждением конечных результатов, полученных аналитически и экспериментально различными авторами. При течении в плоских каналах и больших числах Гартмана критическое значение числа Рейнольдса может быть определено

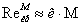,                                                               (1.23)

где к = 250.

Поперечное магнитное поле оказывает сильное стабилизирующее влияние на характер течения жидкости. Магнитное поле интенсивно подавляет пульсации турбулентные и существенно изменяет профиль скоростей. Достаточно при этом напомнить читателю, что при обычном гидродинамическом течении в трубе критическое значение числа Рейнольдса примерно равно 2300.

Способность магнитного поля ламинизировать течение может широко использоваться в прикладных технических задачах. Физически стабилизирующее влияние магнитного поля проще всего объяснить тем фактом, что при всяком возмущении в локальном объеме жидкости возникает электромагнитная сила торможения пропорциональная 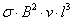. Эта сила гасит возмущение, критическое значение числа Рейнольдса возрастает и область ламинарного течения расширяется. На рис. 1.12 представлена приближенная классификация течения в плоском канале в зависимости от числа Гартмана.

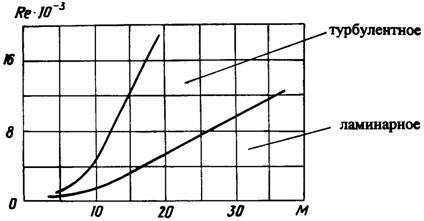
Рис. 1.12