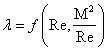1.6. Турбулентное течение в магнитогидродинамических каналах

Турбулентные течения в обычной гидродинамике не могут быть подвергнуты строгому теоретическому анализу, так как турбулентная картина потока не только исключительно сложна, но и непрерывно меняется в деталях. Уравнения Навье–Стокса могут правильно отразить явления в любой точке в данный момент, но совершенно ясно, что попытка применить их к конечному участку течения за конечный промежуток времени абсолютно бесплодны. Поэтому закономерности распределения усредненных скоростей турбулентного течения в каналах, а также сопротивления последних исследуют опытным путем, используя для обобщения данные эксперимента. В магнитной гидродинамике изучение влияния поперечного магнитного поля на турбулентное течение жидкости в канале является наиболее сложным. Как и в обычной гидродинамике в прикладной технической магнитной гидродинамике преимущественно применяются полуэмпирические методы исследования, основанные на установлении определяющих критериев и параметров. Как и прежде нам стоит ограничиться только физической стороной дела.

Поперечное магнитное поле, воздействуя на турбулентный поток проводящей жидкости в канале, приводит к изменению профиля скорости по сечению канала и подавлению турбулентных пульсаций. При малых числах Гартмана профиль скорости по своей форме близок к обычному гидродинамическому, т.е магнитное поле не увеличивает сколько-нибудь существенно градиент скорости у стенок канала, но способствует подавлению турбулентных пульсаций. Поэтому при заданном числе Рейнольдса Re наблюдается уменьшение коэффициента сопротивления по сравнению с его величиной в обычной гидродинамике. Наоборот, при малых М и больших Re, т.е. при , влиянием магнитного поля можно пренебречь и рассчитывать гидравлическое сопротивление канала по формулам обычной гидродинамики. В этом случае электромагнитные силы  влияют только на энергетический баланс потока в целом и не влияют на распределение скоростей.

При больших числах Гартмана эффект увеличения градиента скорости у стенок канала превалирует над эффектом подавления турбулентных пульсации. Поэтому в этом случае в определенном диапазоне чисел Рейнольдса наблюдается увеличение коэффициента сопротивления.

С точки зрения технических задач магнитной гидродинамики область турбулентного потока может быть разделена на две зоны: в первой зоне, соответствующей малым числам М, магнитное поле уменьшает коэффициент сопротивления по сравнению с его величиной в обычной гидродинамике, во второй зоне, соответствующей большим числам М – увеличивает.

Из всего сказанного следует, в частности, что коэффициент сопротивления λ в магнитной гидродинамике недопустимо рассчитывать по формулам обычной гидродинамики. На основании достаточно многих экспериментальных данных коэффициент сопротивления определяется с необходимой точностью зависимостью . При значениях числа »10^-3 коэффициент λ можно определять по эмпирической формуле

,                                                   (1.24)

где λ₀ – коэффициент сопротивления в обычной гидродинамике.

В данной главе были изложены основные, но далеко не все явления при течении проводящей жидкости в каналах при весьма упрощающих допущениях. В действительности реальные каналы имеют конечные размеры, а магнитное поле в продольном направлении также имеет конечную длину. Это дополнительно вызывает на входе и выходе из канала краевые эффекты. Конечные размеры канала и проводимость стенок канала даже при ламинарном течении вызывают дополнительные трудности при решении и анализе. Вместе с тем качественный анализ магнитогидродинамических явлений позволил достаточно наглядно продемонстри­ровать основные эффекты, возникающие при движении проводящей жидкости в поперечном магнитном поле. Конечно, в силу специфики данного пособия здесь не могли быть рассмотрены вопросы, связанные с возникновением магнитогидродинамических волн, имеющих важное практическое применение, а также многие другие задачи.