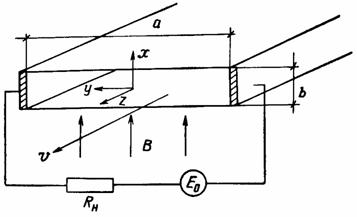
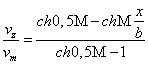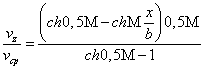1.3. Ламинарные и турбулентные МГД–течения в каналах

Аналитическое рассмотрение магнитогидродинамической задачи по  исследованию течения проводящей жидкости возможно только для случая ламинарного потока. При этом наиболее простой и наглядной является задача по определению течения в плоском канале.

Схема плоского канала показана на рис. 1.4. Две стенки при  являются непроводящими (полюсы магнита), а две других при  – хорошо проводящими электродами, R_H – сопротивление нагрузки, Е₀ – источник ЭДС. Канал считается очень длинным в направлении оси z.

Рис. 1.4

Для решения задачи необходимо выполнить некоторые преобразования в уравнении индукции (1.7) и в правой части уравнения Навье–Стокса (1.2).

Представим первый член правой части уравнения (1.7) в виде

.                                          (1.15)

Поскольку канал очень длинный можно положить , откуда

                                                               (1.16)

 Так как магнитное поле стационарно уравнение (1.7) принимает вид:

                                                     (1.17)

 Выражение для пондеромоторной силы в (1.2) преобразуем следующим образом:

      (1.18)

С учетом последнего правая часть уравнения (1.2) получает вид

.                                                (1.19)

Уравнения (1.19) и (1.17) с учетом граничных условий для В и v позволяют для ламинарного режима течения определить распределение скорости и плотности электрического тока в потоке, а также выделить потери мощности, обусловленные вязким трением и с учетом влияния, которое оказывает на них магнитное поле.

Не затрудняя читателя подробным решением задачи для канала с a»b (наиболее простой случай для решения) представим решение в окончательном виде:

;                                                (1.20)

,                                      (1.21)

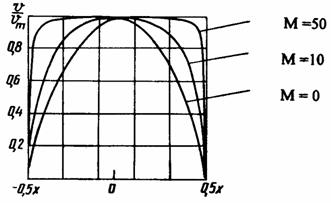
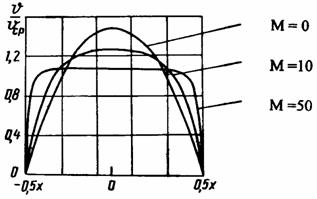
где v_m – максимальная скорость течения; v_ср – средняя скорость потока.

Профили скорости, построенные по (1.20) и (1.21) представлены на рис. 1.5 и рис. 1.6.

Рис. 1.5

Рис. 1.6

Из представленных графиков явственно следует, что при постоянной средней скорости магнитное поле приводит к уплощению профиля и увеличению градиента скорости у стенок канала. Последнее обстоятельство приводит к возрастанию потерь, обусловленных вязким трением. Это является одним из важных проявлений МГД–эффектов при течении в каналах с поперечным магнитным полем.

Теперь можно более подробно рассмотреть МГД–эффекты 1–го и 2–го рода для случая течения жидкости в режиме генерирования электроэнергии, т.е. в режиме генератора (Е₀ = 0).