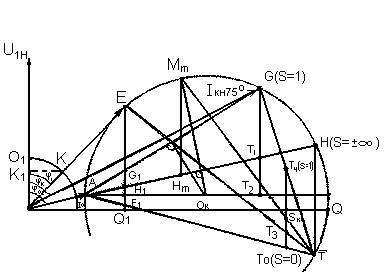
Рис. 2.2. Круговая диаграмма асинхронного двигателя.

 Соединяют точки A и G. К середине отрезка AG восстанавливают перпендикуляр и продолжают его до пересечения в точке О_к с горизонталью, проведенной из точки А. Точка О_к будет являться центром круговой диаграммы. Проводят окружность, проходящую через точки А и G, с центром в точке О_к.
    Далее опускают перпендикуляр из точки G на диаметр окружности получают точку T₂; отрезок GT₂ делят в отношении

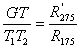
где R₁₇₅ — активное сопротивление фазы обмотки статора (указано на стенде), пересчитанное для температуры 75°С;
R₂₇₅'=R_К75—R₁₇₅ — активное сопротивление фазы обмотки ротора, приведенное к виткам фазы статора, при t = 75°C.
    Через точки А и 7, проводят прямую до пересечения с окружностью в точке Н, в которой скольжение s= ± ∞.
    В круговой диаграмме линии AG, АН и OQ имеют следующие названия:
    AG — линия механической мощности (для двигателя это полезная мощность на валу Р₂);
    АН — линия электромагнитной мощности Р₁₂ и электромагнитного момента М;
  OQ — линия электрической мощности (для двигателя это потребляемая мощность из сети Р₁ ).
      Для определения значений М, Р₁ , Р₂, cosφ₁ , η, s, n₂ при номинальном токе статора I_1H из точки О делают засечку отрезком OE=I_1H/µ_I . Из точки E опускают перпендикуляр на ось абсцисс и получают точку Q₁. Отрезки, отсекаемые на EQ₁ линиями механической, электромагнитной и потребляемой мощности, в масштабе мощности соответственно равны Р₂ , P₁₂ и P₁  .
    Мощность на валу двигателя, кВт; P₂ = µ_рEG₁, где µ_p =3 U_1Hф  µ₁ 10^-3 — масштаб мощности, кВт/мм.
Электромагнитная мощность, кВт: P₁₂ = µ_рEH₁
Потребляемая двигателем мощность из сети, кВт: P₁ = µ_рEQ₁
Момент на валу двигателя Н·м: M =µ_mEH₁, где

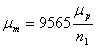
— масштаб момента, (Н∙м)/мм. Здесь n₁ = 60ƒ₁/p — синхронная частота вращения, об/мин; р — число пар полюсов двигателя; ƒ₁ — частота тока сети, Гц; U_1Hф — номинальное фазное напряжение. Длина всех отрезков берется в мм. Для определения скольжения строится шкала скольжений.
    Для этого из точки Н проводится вертикальная линия до пересечения с окружностью в точке Т; точку Т соединяют лучами с точками А и G. Затем проводят шкалу скольжения Т₀Т₄ , параллельно ТН на таком удалении от ТН, чтобы отрезок T₀T₄, удобно делился на 10 равных частей; в точке Т₀ s = 0, в точке Т₄  s=1.
    Чтобы найти скольжение, соответствующее точке Е круговой диаграммы, нужно соединить ее с точкой Т; тогда линия ТЕ отсечет отрезок Т₀Т₃. Скольжение в точке Е (в относительных единицах) будет равно s = T₀T₃/T₀T₄.
    Значение частоты вращения ротора вычисляется по формуле
n₁= n₁(1— s) .
    Для определения коэффициента мощности строится шкала cosφ₁: проводится 1/4 вспомогательной окружности радиусом 4—5 см с центром в точке О. Радиус ОО₁, совпадающий с осью ординат, и будет шкалой cosφ₁: в точке О cosφ₁=0, в точке O₁ cosφ₁=1. Вспомогательная окружность пересекает вектор тока ОЕ в точке K, тогда проекция отрезка ОК на ось ординат OK₁ = cosφ₁.
    КПД двигателя рассчитывается по формуле:

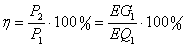
    Более точно можно определить кпд косвенным методом (см. работу № 1).
    Потери в двигателе, кВт, выражаются следующими отрезками:
– электрические потери в обмотке статора P_M1 = µ_рH₁F₁ ;
– электрические потери в обмотке ротора P_M2 = µ_рG₁H₁ ;
– потери в стали P_ст = µ_рF₁Q₁ .