|
22. Магнитное поле задано на
плоскости z комплексной потенциальной функцией
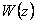 .
Преобразованное магнитное поле в плоскости .
Преобразованное магнитное поле в плоскости
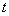 описывается
комплексной потенциальной функцией описывается
комплексной потенциальной функцией
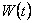 . .
Определить:
а) функцию преобразования
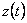 ,
связывающую плоскости ,
связывающую плоскости
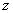 и и
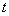 ; ;
б) функции потока и скалярного
магнитного потенциала
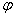 и и
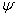 ; ;
в) построить линию потока в
эквипотенциальную линию через точку
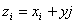 ; ;
г) рассчитать и построить в
удобном для анализа масштабе зависимость модуля напряженности
магнитного поля 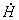 от
расстояния от
расстояния 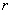 точки
наблюдения до точки точки
наблюдения до точки 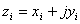 при
перемещении при
перемещении
вдоль прямой
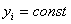 ; ;
д) вычислить магнитный поток
через плоский линейный контур Шириной
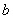 единичной
длины в направлении, перпендикулярном плоскости поля. Контур
располагается в плоскости единичной
длины в направлении, перпендикулярном плоскости поля. Контур
располагается в плоскости
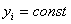 и
его ось совпадает с осью ординат. и
его ось совпадает с осью ординат.
23. Магнитное поле возбуждается
током 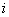 .
Его величина и расположение относительно начала координат,
задаваемое вектором—комплексом .
Его величина и расположение относительно начала координат,
задаваемое вектором—комплексом
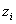 ,
сохраняются такими же, как и в задаче № 22, однако теперь нижняя
половина плоскости, задаваемая неравенством ,
сохраняются такими же, как и в задаче № 22, однако теперь нижняя
половина плоскости, задаваемая неравенством
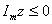 ,
представляет собой ферромагнитное полупространство с ,
представляет собой ферромагнитное полупространство с
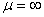 . .
Определить:
а) общее выражение для
комплексной потенциальной функции
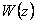 (оно
должно совпасть с приведенным в табл. выражением); (оно
должно совпасть с приведенным в табл. выражением);
б) то же, что и в пунктах г) и
д) задачи № 22. |