|
Следует иметь в виду, что
исследованию подлежат потенциальные (безвихревые) магнитные поля,
для которых выполняются условия
 ,
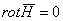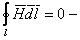
для искомых векторов поля или уравнения Лапласа;
 ,
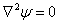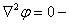
для вспомогательных функций скалярного
магнитного потенциала и функции потока. При наличии в области
вихрей, где  ,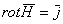
последние должны быть исключены из области поля искусственным
путем (см. ниже).
Функции, удовлетворяющие
уравнению Лапласа, принято называть гармоническими. Совокупность
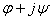 двух
гармонических функций, описывающих одно и то же магнитное поле (или
поле иной физической природы), образует комплексную
потенциальную функцию
 ,
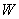зависящую от комплексной переменной
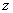 и
относящуюся к так называемым (в теории функций комплексного
переменного) аналитическим функциям.
Производная от аналитических
функций
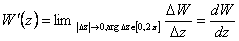(1)
не зависит от аргумента
приращения  .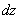
Имея в виду, что любое комплексное число в геометрическом смысле
эквивалентно некоторому вектору, определим расчетное выражение
для приращения .
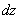Оно имеет вид |
