|
Так как
 (6)
(6)
то,
заменяя в последнем
выражении
единичные орты
 , ,
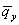 , ,
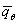 , ,
 на на
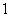 , ,
 , ,
 , ,
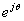 соответственно,
нетрудно получить соотношения, связывающие между собой
составляющие напряженности магнитного поля в обеих системах
координат соответственно,
нетрудно получить соотношения, связывающие между собой
составляющие напряженности магнитного поля в обеих системах
координат
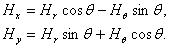 (7)
(7)
Напряжённость магнитного поля,
если известна производная от комплексного потенциала
 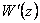 ,
определяется из соотношения ,
определяется из соотношения
 (8)
(8)
Интеграл по замкнутому контуру

(9)
не содержащему внутри себя
особых точек (в таких точках производная обращается в нуль или
бесконечность), всегда равен нулю. Упомянутые выше особые точки
совпадают с местом расположения линейных токов. Вне этих
точек и условно непроницаемых перегородок (кривых) между этими
точками функция комплексного потенциала
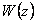 однозначна,
а ее производная отлична от нуля и бесконечности. Так как однозначна,
а ее производная отлична от нуля и бесконечности. Так как
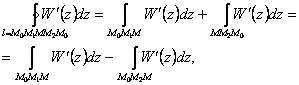 (10)
(10)
а в целом интеграл по замкнутому
контуру  равен
нулю, то следует, что в потенциальных полях криволинейные
интегралы равен
нулю, то следует, что в потенциальных полях криволинейные
интегралы
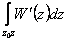
|