|
|
ЛАБОРАТОРНАЯ РАБОТА №5
ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
В ТРАНСФОРМАТОРЕ
Цель работы – изучение метода математического моделирования
дифференциальных уравнений (ДУ) трансформатора (ТР) и исследование на ПК
режимов: включения в сеть на холостом ходу (XX); внезапного короткого
замыкания (КЗ)
и работы при нагрузке.
Электромагнитные процессы в отдельных фазах при подключении напряжения к трёхфазному трансформатору (ТР) протекают аналогично, как и
у однофазного трансформатора [1]. Отличие лишь в том, что эти процессы
для различных фаз ТР сдвинуты на угол
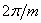 и
в фазном напряжении при соединении обмоток в звезду из-за магнитного
насыщения появляется 3-я
гармоника, которая уменьшает максимальное значение потока
по сравнению
с однофазным трансформатором. Это, а также неодинаковая
степень насыщения стержней сердечника приводят к уменьшению
максимального значения тока при включении трехфазного трансформатора.
При симметричной
нагрузке трехфазные ТР в большинстве случаев исследуются для одной из
его фаз, что значительно упрощает создание математической модели. и
в фазном напряжении при соединении обмоток в звезду из-за магнитного
насыщения появляется 3-я
гармоника, которая уменьшает максимальное значение потока
по сравнению
с однофазным трансформатором. Это, а также неодинаковая
степень насыщения стержней сердечника приводят к уменьшению
максимального значения тока при включении трехфазного трансформатора.
При симметричной
нагрузке трехфазные ТР в большинстве случаев исследуются для одной из
его фаз, что значительно упрощает создание математической модели.
Часть
I
ИССЛЕДОВАНИЕ ХОЛОСТОГО ХОДА
Введение
В первой части работы исследуется зависимость тока
XX
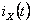 от
начальной
фазы от
начальной
фазы 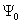 включения
гармонического напряжения включения
гармонического напряжения 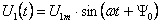 на
первичную обмотку двухобмоточного трансформатора. на
первичную обмотку двухобмоточного трансформатора.
Определяется угол
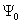 включения
напряжения включения
напряжения
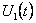 ,
при котором сразу
устанавливается режим с синусоидально
изменяющимся током ,
при котором сразу
устанавливается режим с синусоидально
изменяющимся током 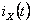 и
наиболее неблагоприятный угол и
наиболее неблагоприятный угол
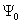 ,
при котором возникает переходный процесс и амплитуда тока имеет
максимальное (ударное) значение ,
при котором возникает переходный процесс и амплитуда тока имеет
максимальное (ударное) значение
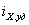 .
Рассчитываются
и определяются моделированием на ПК время .
Рассчитываются
и определяются моделированием на ПК время
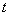 от
начала переходного процесса до установившегося и время нарастания тока от
начала переходного процесса до установившегося и время нарастания тока
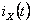 от
0 до от
0 до
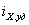 . .
Согласно закону электромагнитной индукции напряжение на первичной
обмотке ТР определяется из уравнения
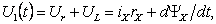
которое в форме Коши имеет вид
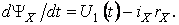 (5.1)
(5.1)
Так как
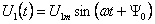 ,
то (5.1) в относительных единицах (о.е)
базового
напряжения ,
то (5.1) в относительных единицах (о.е)
базового
напряжения 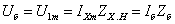 записывается
как записывается
как
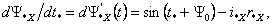 (5.2)
(5.2)
где
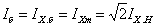 и и
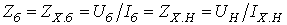 –
базовый (максимальный)
ток и базовое (полное) сопротивление при гармоническом напряжении; –
базовый (максимальный)
ток и базовое (полное) сопротивление при гармоническом напряжении;
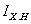 –
действующее значение тока
XX
при номинальном фазовом
напряжении –
действующее значение тока
XX
при номинальном фазовом
напряжении
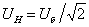 в
установившемся режиме; в
установившемся режиме; 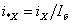 –
относительный
ток
XX; –
относительный
ток
XX;
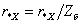 –
относительное сопротивление
XX; –
относительное сопротивление
XX;
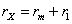 –
активное
сопротивление
XX,
состоящее из активных сопротивлений –
активное
сопротивление
XX,
состоящее из активных сопротивлений
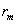 и и
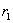 ,
определяемых
потерями в стали и в первичной обмотке; ,
определяемых
потерями в стали и в первичной обмотке;
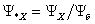 –
относительное
потокосцепление
XX; –
относительное
потокосцепление
XX;
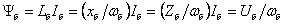 –
базовое потокосцепление; –
базовое потокосцепление;
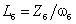 , ,
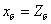 и и
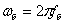 –
базовые значения индуктивности,
индуктивного сопротивления и угловой частоты при базовой частоте сети –
базовые значения индуктивности,
индуктивного сопротивления и угловой частоты при базовой частоте сети
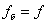 ; ;
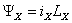 –
потокосцепление
XX; –
потокосцепление
XX;
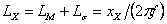 –
индуктивность
XX,
состоящая из индуктивностей –
индуктивность
XX,
состоящая из индуктивностей 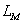 и и
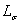 ,
определяемых магнитными
потоками взаимоиндукции и рассеяния; ,
определяемых магнитными
потоками взаимоиндукции и рассеяния;
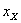 –
индуктивное сопротивление; –
индуктивное сопротивление;
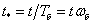 –
относительное время, рад.; –
относительное время, рад.;
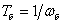 –
базовое время, с;
Ψ0
– угол включения, рад; –
базовое время, с;
Ψ0
– угол включения, рад;
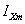 –
амплитуда тока
XX. –
амплитуда тока
XX.
Ток
XX
в переходном процессе [1] равен
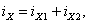 (5.3)
(5.3)
где
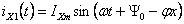 (5.4)
(5.4)
–
установившийся (вынужденный)
синусоидальный ток, обусловленный напряжением
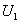 ; ;
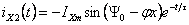 (5.5)
(5.5)
–
апериодический (свободный) ток,
обусловленный индуктивностью хX;
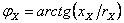 –
фазовый угол
XX; –
фазовый угол
XX;
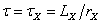 –
постоянная времени затухания
тока
iX. –
постоянная времени затухания
тока
iX.
На основании (5.4) и (5.5) очевидно, что в
начальный момент времени 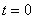 ток ток
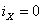 (5.3),
т.е. начальное значение тока (5.3),
т.е. начальное значение тока
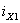 равно
по величине и обратно
по знаку начальному значению тока равно
по величине и обратно
по знаку начальному значению тока
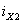 . .
Известно [1 и 2], что если в момент времени
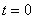 напряжение напряжение
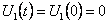 ,
то угол ,
то угол 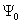 будет
наиболее неблагоприятным, т.е. через некоторое
время произойдет всплеск тока будет
наиболее неблагоприятным, т.е. через некоторое
время произойдет всплеск тока
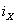 до
ударного значения до
ударного значения
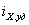 ,
который
при отсутствии магнитного насыщения приблизительно
равен ,
который
при отсутствии магнитного насыщения приблизительно
равен 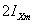 .
Если же в
этот момент времени напряжение .
Если же в
этот момент времени напряжение
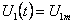 ,
т.е. равно его амплитуде, то ,
т.е. равно его амплитуде, то
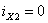 и
в цепи сразу возникает установившийся режим, т.е. и
в цепи сразу возникает установившийся режим, т.е.
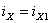 .
Из изложенного
следует, что если .
Из изложенного
следует, что если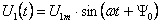 ,
то угол ,
то угол
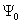 наиболее
неблагоприятный, когда он
равен нулю, а благоприятный согласно (5.5) равен наиболее
неблагоприятный, когда он
равен нулю, а благоприятный согласно (5.5) равен
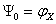 .
Если же .
Если же 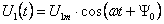 ,
то соответственно ,
то соответственно
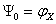 и и
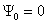 . .
|
|
Исследование холостого хода
5.1 Составление структурных блок-схем
5.2 Расчет коэффициентов решающих блоков
5.3 Программа и порядок выполнения работ
Исследование короткого замыкания трансформатора
5.4 Составление структурной блок-схемы
5.5 Расчет коэффициентов решающих блоков
5.6 Программа и порядок выполнения работ
Исследование трансформатора при нагрузке
5.7 Составление структурной блок-схемы
5.8
Расчет
коэффициентов решающих блоков
5.9
Программа и порядок выполнения работ
5.10 Задание к коллоквиуму
5.11 Требования к оформлению отсчета
5.13 Вопросы к защите работы
|