|
|
ЛАБОРАТОРНАЯ РАБОТА №6
ИССЛЕДОВАНИЕ ВХОЖДЕНИЯ В СИНХРОНИЗМ
СИНХРОННОГО ДВИГАТЕЛЯ
Цель работы – изучение метода математического моделирования дифференциальных уравнений (ДУ) и исследование на ПК процесса синхронизации
синхронных двигателей (СД) с возбужденным и невозбужденным ротором.
Введение
При расчетах, проектировании и испытаниях СД первостепенное значение имеет определение предельного момента
нагрузки
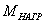 ,
при котором
происходит надежное втягивание в синхронизм. Такой момент нагрузки называется
моментом входа в синхронизм ,
при котором
происходит надежное втягивание в синхронизм. Такой момент нагрузки называется
моментом входа в синхронизм 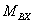 .
Момент .
Момент 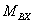 ,
а следовательно, и
номинальная мощность ,
а следовательно, и
номинальная мощность
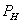 СД
с асинхронным пуском, зависят как от характера
изменения, так и от значений моментов в зоне синхронизации асинхронного СД
с асинхронным пуском, зависят как от характера
изменения, так и от значений моментов в зоне синхронизации асинхронного
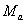 и
синхронизирующего и
синхронизирующего 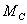 ,
а также от момента инерции ,
а также от момента инерции 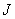 ротора и момента нагрузки. Одно и тоже значение ротора и момента нагрузки. Одно и тоже значение
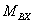 может быть получено при
выборе различных сочетаний пусковых и угловых
характеристик, соотношение и связь между которыми определяют
энергетические показатели в синхронном
режиме. может быть получено при
выборе различных сочетаний пусковых и угловых
характеристик, соотношение и связь между которыми определяют
энергетические показатели в синхронном
режиме.
Процесс вхождения ротора СД в синхронизм является переходным электромеханическим процессом и описывается системой нелинейных ДУ.
Поскольку механическая постоянная времени в электрических машинах
превышает электромагнитные постоянные времени обмоток статора и ротора,
а в
рассматриваемых ниже СД это превышение значительно, поэтому для исследования вхождения в синхронизм используют не всю систему уравнений, а
лишь уравнение движения ротора, считая при
этом, что электромагнитные процессы протекают значительно быстрее
механических, а динамические моментно-частотные
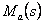 и
моментно-угловые и
моментно-угловые 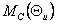 характеристики
тождественны статическим. Здесь характеристики
тождественны статическим. Здесь
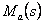 и и
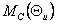 – зависимости моментов асинхронного от
скольжения ротора – зависимости моментов асинхронного от
скольжения ротора 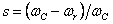 и
синхронизирующего от угла
нагрузки и
синхронизирующего от угла
нагрузки
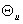 ,
рад. между осями продольного поля и полюсов ; ,
рад. между осями продольного поля и полюсов ;
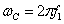 –
электрическая угловая частота вращения поля статора, –
электрическая угловая частота вращения поля статора,
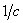 ; ; 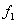 –
частота сети,
Гц; –
частота сети,
Гц;
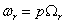 –
электрическая угловая частота вращения ротора, –
электрическая угловая частота вращения ротора,
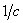 ; ; 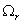 –
механическая
частота вращения ротора, –
механическая
частота вращения ротора,
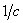 . .
Исходным уравнением для исследования вхождения в синхронизм СД
с асинхронным пуском является уравнение движения ротора, которое в абсолютных
единицах (а.е.) измерения, имеет вид 60
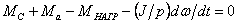
или
 (6.1)
(6.1)
где
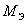 –
электромагнитный момент, Н∙м; –
электромагнитный момент, Н∙м;
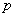 –
число пар полюсов; –
число пар полюсов; 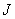 –
суммарный момент инерции, кг∙м2.
При номинальном моменте нагрузки –
суммарный момент инерции, кг∙м2.
При номинальном моменте нагрузки
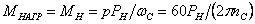 ,
Н∙м,
где ,
Н∙м,
где
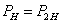 –
активная номинальная полезная мощность, Вт; –
активная номинальная полезная мощность, Вт;
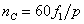 –
синхронная частота вращения ротора, –
синхронная частота вращения ротора,
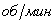 . .
Для явнополюсного возбужденного (с активным ротором) СД при частотах вращения, близких к синхронной (при малых скольжениях), синхронизирующий момент можно представить суммой моментов, т.е.
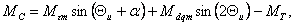 (6.2)
(6.2)
где
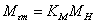 и и
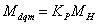 –
максимальные значения основного
синхронизирующего и реактивного моментов; –
максимальные значения основного
синхронизирующего и реактивного моментов;
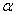 – угол сдвига (рад) между
характеристиками СД – угол сдвига (рад) между
характеристиками СД 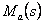 и и
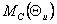 или или 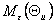 и и  (рис. 6.1); (рис. 6.1);
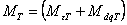 – тормозной момент (для СД – тормозной момент (для СД
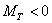 ),
зависящий от параметров
СД, который определяется согласно изложенному в
[6,7]; ),
зависящий от параметров
СД, который определяется согласно изложенному в
[6,7]; 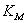 и и
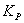 – коэффициенты
кратности моментов основного синхронизирующего и реактивного, о.е.; – коэффициенты
кратности моментов основного синхронизирующего и реактивного, о.е.; 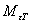 –
тормозной момент, обусловленный
активным сопротивлением
статора и
возбуждением ротора, Н∙м; –
тормозной момент, обусловленный
активным сопротивлением
статора и
возбуждением ротора, Н∙м; 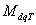 –
тормозной момент, обусловленный неравенством магнитных проводимостей по
осям –
тормозной момент, обусловленный неравенством магнитных проводимостей по
осям
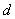 , ,
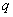 и
активным сопротивлением статора, Н∙м. Если активное сопротивление
статора принять равным нулю,
то и
активным сопротивлением статора, Н∙м. Если активное сопротивление
статора принять равным нулю,
то
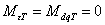 . .
Асинхронный момент в зоне синхронизации изменяется прямо
пропорционально
скольжению, т.е.
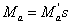 (6.3)
(6.3)
где 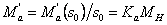 – крутизна пусковой механической характеристики (рис. 6.1); – крутизна пусковой механической характеристики (рис. 6.1);
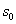 –
начальное скольжение ротора на линейной части
характеристики –
начальное скольжение ротора на линейной части
характеристики 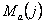 ; ;
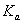 – коэффициент кратности асинхронного момента. Угол – коэффициент кратности асинхронного момента. Угол 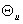 характеризующий
нагрузку СД, изменяется в процессе синхронизации в широких пределах и
определяется по формуле характеризующий
нагрузку СД, изменяется в процессе синхронизации в широких пределах и
определяется по формуле
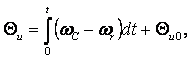 (6.4)
(6.4)
где 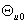 –
начальный угол нагрузки. –
начальный угол нагрузки.
На основании (6.4) устанавливается связь
скольжения 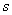 с
углом нагрузки с
углом нагрузки
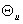 и
частотой вращения ротора и
частотой вращения ротора 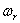 ,
т.е. ,
т.е. 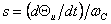 и и
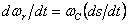 ,
тогда (6.1) в зоне синхронизации с учётом (6.2) и (6.3) можно записать
как ,
тогда (6.1) в зоне синхронизации с учётом (6.2) и (6.3) можно записать
как
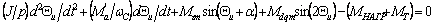 (6.5) (6.5)
Принимая в качестве базисных единиц для СД
основной максимальный момент 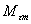 ,
собственную угловую частоту колебаний ,
собственную угловую частоту колебаний
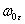 и
время и
время 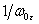 ,
т.е. ,
т.е.
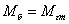 , ,
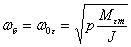 и и
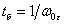 ,
можно записать (6.5) в о.е.
измерения и привести к нормальной форме Коши, тем самым
преобразовав его к виду, удобному для моделирования, ,
можно записать (6.5) в о.е.
измерения и привести к нормальной форме Коши, тем самым
преобразовав его к виду, удобному для моделирования,
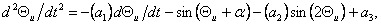 (6.6)
(6.6)
где
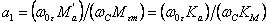 –
коэффициент демпфирования, о.е.; –
коэффициент демпфирования, о.е.;
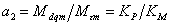 –
коэффициент реактивности, о.е.; –
коэффициент реактивности, о.е.;
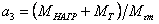 –
коэффициент нагрузки, о.е.; –
коэффициент нагрузки, о.е.;
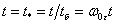 –
время, о.е. –
время, о.е.
Для неявнополюсного возбуждённого СД, в котором
отсутствует реактивный момент
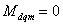 ,
уравнение (6.6) в о.е. измерения имеет вид ,
уравнение (6.6) в о.е. измерения имеет вид
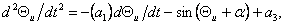 (6.7)
(6.7)
где
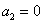 ; ;
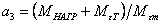 –
коэффициент нагрузки, о.е. –
коэффициент нагрузки, о.е.
Для реактивного невозбуждённого (с пассивным
ротором) СД, в котором отсутствует основной момент
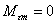 ,
принимая в качестве базисных единиц ,
принимая в качестве базисных единиц 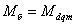 , ,
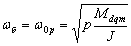 и и
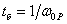 ,
уравнение (6.6) в о.е. измерения принимает вид ,
уравнение (6.6) в о.е. измерения принимает вид
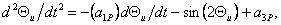 (6.8)
(6.8)
где  ; ;
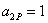 ; ;
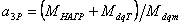 и и
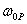 –
коэффициенты демпфирования, нагрузки и собственная угловая
частота реактивного СД в о.е. измерения. –
коэффициенты демпфирования, нагрузки и собственная угловая
частота реактивного СД в о.е. измерения.
Механические процессы, описываемые уравнениями
(6.6), (6.7) или (6.8) протекают соответственно в
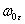 или или
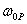 раз
медленнее реальных. раз
медленнее реальных.
|
|
Введение
6.1 Составление структурных блок-схем
6.2 Расчет коэффициентов решающих блоков
6.3
Методические указания
6.4 Программа и порядок выполнения работ
6.5 Задание к коллоквиуму
6.6 Требования к оформлению отсчета
6.7 Вопросы к защите работы
|