|
|
ЛАБОРАТОРНАЯ РАБОТА № 7
ИССЛЕДОВАНИЕ ПУСКОВЫХ, СИНХРОНИЗИРУЮЩИХ И РАБОЧИХ СВОЙСТВ СИНХРОННЫХ
МИКРОДВИГАТЕЛЕЙ
Введение
Двигатели СДПМ и СРД находят широкое применение в качестве
электроприводов малой мощности, в частности, для различного рода
лентопротяжных механизмов.
Электромеханические процессы, происходящие при
пуске, синхронизации и в рабочем режиме СДПМ с учетом общепринятых в
теории синхронных машин допущений, описываются системами нелинейных
уравнений в координатных осях
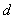 , ,
 ,
жестко связанных с ротором. Исследование значительно упрощается,
если все параметры входящие в системы уравнений выразить в относительных
единицах (о.е.) измерения, т.е. относительно базисных параметров. Расчёт
базисных параметров указан в табл. 7.1. Следует заметить, что в о.е.
измерения индуктивности и соответствующие им индуктивные сопротивления
имеют одинаковые числовые значения. Все параметры роторных цепей
приводятся к числу фаз и витков обмотки статора. При записи системы
уравнений принято, что ось
q
опережает ось
d.
Постоянный
магнит заменяется одновитковым контуром без потерь, включенным на
источник постоянного тока. В этом случае система имеет вид и состоит из
уравнений: ,
жестко связанных с ротором. Исследование значительно упрощается,
если все параметры входящие в системы уравнений выразить в относительных
единицах (о.е.) измерения, т.е. относительно базисных параметров. Расчёт
базисных параметров указан в табл. 7.1. Следует заметить, что в о.е.
измерения индуктивности и соответствующие им индуктивные сопротивления
имеют одинаковые числовые значения. Все параметры роторных цепей
приводятся к числу фаз и витков обмотки статора. При записи системы
уравнений принято, что ось
q
опережает ось
d.
Постоянный
магнит заменяется одновитковым контуром без потерь, включенным на
источник постоянного тока. В этом случае система имеет вид и состоит из
уравнений:
равновесия напряжений обмоток статора и ротора –
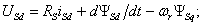
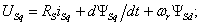
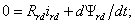 (7.1)
(7.1)
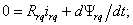
потокосцеплений обмоток статора и ротора –
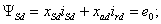
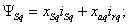
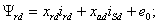 (7.2) (7.2)
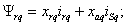
движения ротора
–
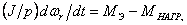 (7.3)
(7.3)
где
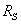 и и
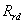 , ,
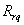 –
активные сопротивления обмотки статора и обмотки ротора при
эквивалентной её замене по осям –
активные сопротивления обмотки статора и обмотки ротора при
эквивалентной её замене по осям
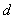 , ,
 ; ;
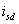 , ,
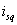 и и
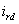 , ,
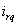 –
токи статора и ротора по осям , –
токи статора и ротора по осям ,
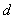  ; ;
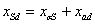 , ,
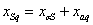 и и
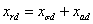 , ,
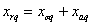 –
полные индуктивные сопротивления фаз статора и ротора по осям –
полные индуктивные сопротивления фаз статора и ротора по осям
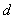 , ,
 ; ;
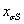 и и
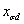 , ,
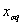 –
индуктивные сопротивления рассеяния обмоток статора и ротора по осям –
индуктивные сопротивления рассеяния обмоток статора и ротора по осям
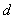 , ,
 ; ;
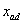 , ,
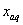 –
синхронные индуктивные сопротивления реакции якоря по осям –
синхронные индуктивные сопротивления реакции якоря по осям
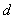 , ,
 ; ;
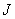 –
момент инерции вращающихся масс; –
момент инерции вращающихся масс;
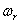 –электрическая
угловая частота вращения ротора; –электрическая
угловая частота вращения ротора;
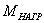 –
момент нагрузки на валу (момент внешних сил); –
момент нагрузки на валу (момент внешних сил);
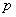 –
количество пар полюсов; –
количество пар полюсов; 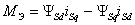 –
электромагнитный момент двигателя; –
электромагнитный момент двигателя;
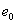 –
ЭДС холостого хода. –
ЭДС холостого хода.
Величина
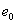 в
(7.2) характеризует потокосцепление поля постоянных магнитов с обмоткой
статора, численно равное в о.е. измерения в
(7.2) характеризует потокосцепление поля постоянных магнитов с обмоткой
статора, численно равное в о.е. измерения
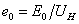 ,
где ,
где 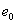 выражено
в масштабе потокосцепления по продольной оси выражено
в масштабе потокосцепления по продольной оси
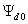 и
характеризует степень возбуждения двигателя от постоянных
магнитов, и
характеризует степень возбуждения двигателя от постоянных
магнитов,
При отсутствии возбуждения со стороны ротора
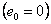 уравнения
(7.1) ÷ (7.3) представляют систему уравнений СРД. уравнения
(7.1) ÷ (7.3) представляют систему уравнений СРД.
Известно, что при симметричной системе
напряжений питания составляющие
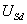 и и
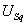 могут
быть представлены в виде могут
быть представлены в виде 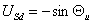 и и
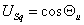 , ,
где
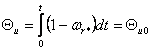 (7.4)
(7.4)
– угол нагрузки между поперечной осью ротора и
вектором напряжения питания;
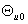 –
начальный угол нагрузки; –
начальный угол нагрузки; 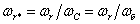 –
относительная электрическая
угловая частота вращения ротора; –
относительная электрическая
угловая частота вращения ротора;
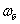 –
базовая частота вращения, равная синхронной частоте вращения ротора –
базовая частота вращения, равная синхронной частоте вращения ротора
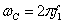 и и
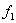 –
частота сети. –
частота сети.
При исследовании двигательного режима работы
машины угол 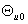 принимается
положительным, когда вектор напряжения питания опережает ось принимается
положительным, когда вектор напряжения питания опережает ось
 ротора.
Используя уравнение (7.4), можно установить связь между углом нагрузки и
частотой вращения ротора ротора.
Используя уравнение (7.4), можно установить связь между углом нагрузки и
частотой вращения ротора
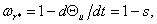 (7.5)
(7.5)
где
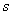 –
скольжение ротора. –
скольжение ротора.
В большинстве случаев значения токов в
эквивалентных обмотках ротора
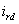 и и
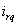 интереса
не представляют. В целях уменьшения числа решающих блоков и повышения
устойчивости модели эти токи можно исключить из рассмотрения в
уравнениях (7.1) и (7.2). Тогда система ДУ в о.е. измерения для
моделирования СДПМ будет иметь вид: интереса
не представляют. В целях уменьшения числа решающих блоков и повышения
устойчивости модели эти токи можно исключить из рассмотрения в
уравнениях (7.1) и (7.2). Тогда система ДУ в о.е. измерения для
моделирования СДПМ будет иметь вид:
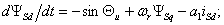
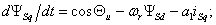
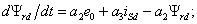
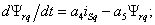 (7.6)
(7.6)
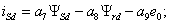
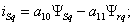
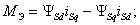
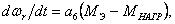
где коэффициенты при переменных в о.е.
измерения равны: 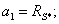 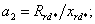 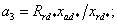 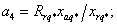 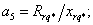 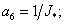 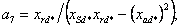 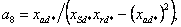 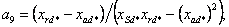 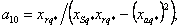 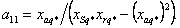
|
|
Введение
7.1 Составление структурных блок-схем
7.2 Расчет коэффициентов решающих блоков
7.3
Методические указания
7.4 Программа и порядок выполнения работ
7.5 Задание к коллоквиуму
7.6 Требования к оформлению отсчета
7.7 Вопросы к защите работы
|